题目内容
13.已知函数f(x)=x2e-2ax(a>0)(1)已知函数f(x)的曲线在x=1处的切线方程为y=-2e-4x+b,求实数a、b的值.
(2)求函数在[1,2]上的最大值.
分析 (1)求导f′(x)=(2x-2ax2)e-2ax,从而可得f′(1)=(2-2a)e-2a═-2e-4;从而解出a,代入求b;
(2)由(1)可得f(x)=x2e-4x,f′(x)=(2x-4x2)e-4x;从而可得f(x)在[1,2]上单调递减;从而求最大值.
解答 解:(1)∵f(x)=x2e-2ax,f′(x)=(2x-2ax2)e-2ax;
∴f′(1)=(2-2a)e-2a═-2e-4;
解得,a=2,
则f(x)=x2e-4x,f(1)=e-4,
故直线y=-2e-4x+b过点(1,e-4);
故b=3e-4;
(2)由(1)得,
f(x)=x2e-4x,f′(x)=(2x-4x2)e-4x;
则当x∈[1,2]时,f′(x)=(2x-4x2)e-4x<0,
故f(x)在[1,2]上单调递减;
故fmax(x)=f(1)=e-4.
点评 本题考查了导数的几何意义及导数的综合应用,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
18.命题p:“a>1,b>1”是命题q:“(a-1)(b-1)>0”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
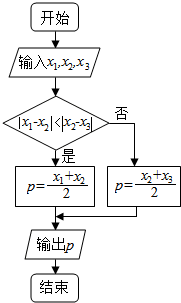 如框图,当x1=6,x2=9,p=8.5时,x3=8.
如框图,当x1=6,x2=9,p=8.5时,x3=8.