题目内容
已知数列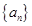 的各项都是正数,且对任意
的各项都是正数,且对任意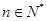 都有
都有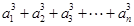
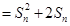 ,其中
,其中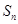 为数列
为数列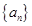 的前
的前 项和.
项和.
(1)求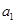 、
、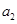 ;
;
(2)求数列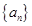 的通项公式;
的通项公式;
(3)设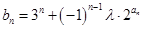 ,对任意的
,对任意的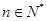 ,都有
,都有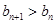 恒成立,求实数
恒成立,求实数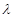 的取值范围.
的取值范围.
(1)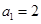 ,
,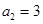 ;(2)
;(2)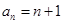 ;(3)
;(3)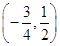 .
.
解析试题分析:(1)分别令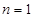 和
和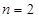 代入题干中的等式求出
代入题干中的等式求出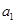 和
和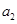 的值;(2)利用定义法进行求解,在原式中利用
的值;(2)利用定义法进行求解,在原式中利用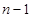 替换
替换 得到
得到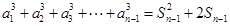 ,将此等式与原式作差得到
,将此等式与原式作差得到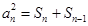
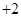 ,再次利用定义法得到数列
,再次利用定义法得到数列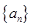 为等差数列,最后利用等差数列的通项公式进行求解;(3)利用
为等差数列,最后利用等差数列的通项公式进行求解;(3)利用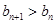 化简得到
化简得到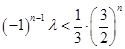 ,对
,对 进行分奇偶讨论求出
进行分奇偶讨论求出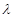 的取值范围.
的取值范围.
试题解析:(1)令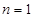 ,则
,则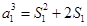 ,即
,即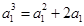 ,所以
,所以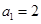 或
或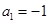 或
或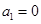 ,
,
又因为数列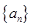 的各项都是正数,所以
的各项都是正数,所以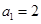 ,
,
令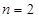 ,则
,则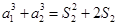 ,即
,即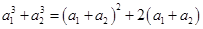 ,解得
,解得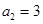 或
或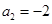 或
或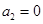 ,
,
又因为数列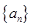 的各项都是正数,所以
的各项都是正数,所以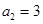 ,
,
(2)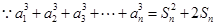 , ①
, ①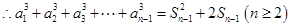 , ②
, ②
由①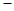 ②得
②得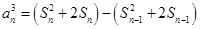 ,
,
化简得到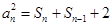 , ③
, ③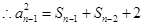 ,④
,④
由③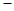 ④得
④得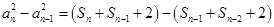 ,
,
化简得到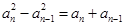 ,即
,即 ,
,
当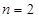 时,
时,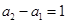 ,所以
,所以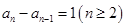 ,
,
所以数列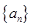 是一个以
是一个以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,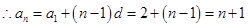 ;
;
(3)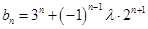 ,
,
因为对任意的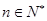 ,都有
,都有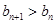 恒成立,即有
恒成立,即有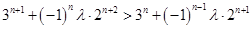 ,
,
化简得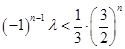 ,
,
当 为奇数时,
为奇数时,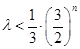 恒成立,
恒成立,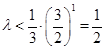 ,即
,即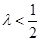 ,
,
当 为偶数时,
为偶数时,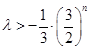 恒成立,
恒成立,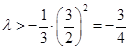 ,即
,即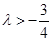 ,
,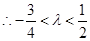 ,故实数
,故实数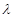 的取值范围是
的取值范围是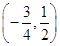 .
.
考点:1.定义法求数列的通项公式;2.数列不等式恒成立;3.分类讨论

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,S4=40,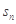 =210,
=210,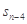 =130,则n=( ).
=130,则n=( ).
| A.12 | B.14 | C.16 | D.18 |
设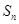 为等差数列
为等差数列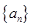 的前
的前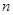 项和,
项和,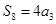 ,
,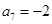 ,则
,则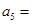 ( )
( )
A.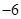 | B.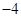 | C.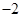 | D. |
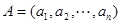 ,
,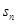 为其前n项和,定义
为其前n项和,定义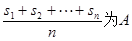 的“凯森和”,若有99项的数列
的“凯森和”,若有99项的数列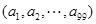 的“凯森和”为1000,则有100项的数列
的“凯森和”为1000,则有100项的数列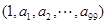 的“凯森和”为 .
的“凯森和”为 .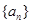 的前
的前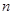 项和为
项和为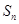 ,且
,且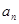 是
是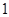 的等差中项,等差数列
的等差中项,等差数列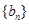 满足
满足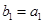 ,
,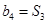 .
.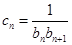 ,数列
,数列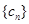 的前
的前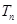 ,证明:
,证明: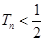 .
.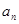 }中,
}中,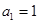 ,前n项和
,前n项和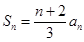 .
.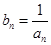 ,求数列{
,求数列{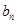 }的前n项和Tn.
}的前n项和Tn.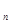 }满足0<a
}满足0<a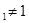 , 且
, 且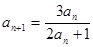 (n
(n N*).
N*). 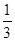 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明. 是首项为2,公比为
是首项为2,公比为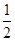 的等比数列,数列
的等比数列,数列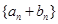 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.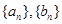 的通项式.
的通项式.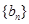 的前
的前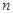 项和
项和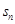 .
.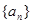 的前
的前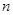 项和为
项和为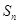 ,
,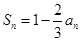 ,则
,则