题目内容
已知数列{ }中,
}中, ,前n项和
,前n项和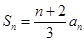 .
.
(I)求a2,a3以及{ }的通项公式;
}的通项公式;
(II)设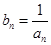 ,求数列{
,求数列{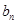 }的前n项和Tn.
}的前n项和Tn.
(I){ }的通项公式为
}的通项公式为 .(II)
.(II)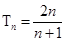 .
.
解析试题分析:(I)通过研究当 时,
时,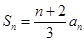 (1),
(1), (2)
(2)
(1)-(2)可得
即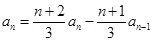

得到 ,验证
,验证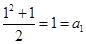 ,适合上式,得出结论.
,适合上式,得出结论.
(II)注意到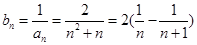 ,所以利用“裂项相消法”求得
,所以利用“裂项相消法”求得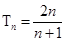 .
.
试题解析:(I)由 与
与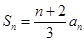 可得
可得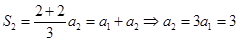 ,
, ,
,
当 时,
时,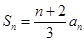 (1),
(1), (2)
(2)
(1)-(2)可得
即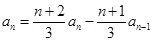

故有 ,
,
而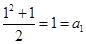 ,所以{
,所以{ }的通项公式为
}的通项公式为
(II)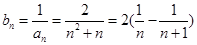 ,
, .
.
考点:数列的通项公式,数列的求和,“裂项相消法”.

练习册系列答案
相关题目
等差数列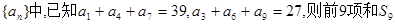 的值为( )
的值为( )
| A.66 | B.99 | C.144 | D.297 |
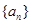 的首项
的首项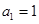 ,其前
,其前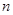 项和
项和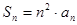
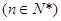 ,则
,则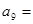 。
。 (2n
(2n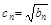 ,
,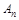 是
是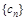 前
前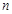 项和,
项和, 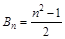 ,当
,当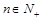 时,试比较
时,试比较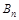 的大小.
的大小.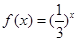 ,等比数列
,等比数列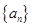 的前n项和为
的前n项和为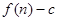 ,数列
,数列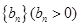 的前n项为
的前n项为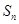 ,且前n项和
,且前n项和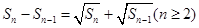 .
. 的通项公式:
的通项公式: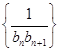 前n项和为
前n项和为 ,问使
,问使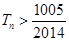 的最小正整数n是多少?
的最小正整数n是多少?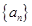 的各项都是正数,且对任意
的各项都是正数,且对任意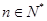 都有
都有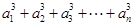
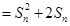 ,其中
,其中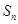 为数列
为数列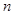 项和.
项和.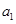 、
、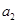 ;
;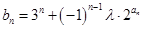 ,对任意的
,对任意的 恒成立,求实数
恒成立,求实数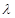 的取值范围.
的取值范围.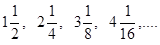 前n项的和。
前n项的和。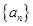 中,
中, ,若在每相邻两项之间各插入一个数,使之成为等差数列,
,若在每相邻两项之间各插入一个数,使之成为等差数列, ,如果
,如果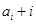 (
(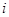 =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数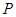 性质”.不论数列
性质”.不论数列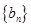 ,且
,且 是
是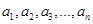 的一个排列;②数列
的一个排列;②数列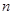 项和
项和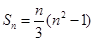 ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“