题目内容
已知函数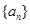 是首项为2,公比为
是首项为2,公比为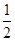 的等比数列,数列
的等比数列,数列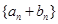 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.
(1)求数列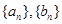 的通项式.
的通项式.
(2)求数列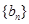 的前
的前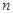 项和
项和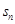 .
.
(1)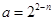 ,bn=2n-4-
,bn=2n-4-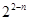 ; (2)Tn=n2-3n-4+
; (2)Tn=n2-3n-4+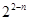 .
.
解析试题分析:(1)直接用等比数列等差数列即可求得数列{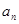 }{bn}的通项公式.
}{bn}的通项公式.
(2)数列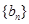 是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
试题解析:(1)∵数列{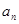 }是首项
}是首项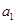 =2,公比q=
=2,公比q=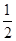 的等比数列,
的等比数列,
∴an=2·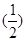 n-1=22-n,
n-1=22-n,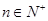 3分
3分
依题意得数列{bn+an}的公差d=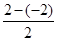 =2,
=2,
∴bn+an=-2+2(n-1)=2n-4,
∴bn=2n-4-22-n,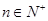 6分
6分
(2)设Sn为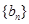 的前n项和,由(1)得 Sn=
的前n项和,由(1)得 Sn=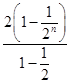 =4
=4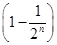 9分
9分
设数列{bn+an}的前n项和为Pn 则 Pn=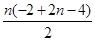 =n(n-3),
=n(n-3),
∴Tn=Pn-Sn=n(n-3)-4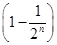 =n2-3n-4+22-n 12分
=n2-3n-4+22-n 12分
考点:等差数列等比数列的通项公式及前n项和公式

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
已知在等差数列 中,
中, 的等差中项为
的等差中项为 ,
,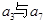 的等差中项为
的等差中项为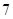 ,则数列
,则数列 的通项公式
的通项公式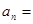 ( )
( )
A. | B. -1 -1 | C. +1 +1 | D. -3 -3 |
已知等比数列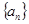 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则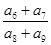 等于( )
等于( )
A.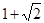 | B.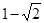 | C.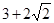 | D. |
 (2n
(2n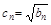 ,
,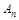 是
是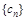 前
前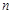 项和,
项和, 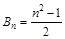 ,当
,当 时,试比较
时,试比较 的大小.
的大小. 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有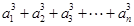
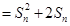 ,其中
,其中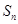 为数列
为数列 项和.
项和.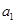 、
、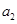 ;
;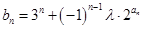 ,对任意的
,对任意的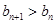 恒成立,求实数
恒成立,求实数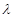 的取值范围.
的取值范围.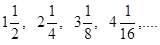 前n项的和。
前n项的和。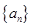 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为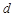 ,
, 为其前
为其前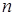 项和,且满足
项和,且满足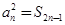 ,
,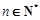 .数列
.数列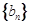 满足
满足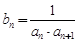 ,
,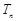 为数列
为数列 项和.
项和.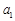 、
、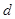 和
和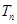 ;
;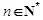 ,不等式
,不等式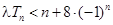 恒成立,求实数
恒成立,求实数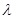 的取值范围;
的取值范围;
 ,使得
,使得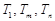 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 中,
中,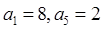 ,若在每相邻两项之间各插入一个数,使之成为等差数列,
,若在每相邻两项之间各插入一个数,使之成为等差数列, 中,如果存在非零的常数
中,如果存在非零的常数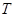 ,使
,使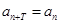 对于任意正整数
对于任意正整数 均成立,就称数列
均成立,就称数列 满足
满足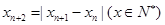 ,若
,若 ,当数列
,当数列 时,则数列
时,则数列