Question

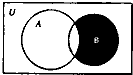已知全集U=R，集合A={x||x|≤1，x∈Z}，B={x|x²-2x=0}，则图中的阴影部分表示的集合为（　　）

A．{-1}

B．{2}

C．{1，2}

D．{0，2}

Answer 1

分析：阴影部分为?_UA∩B，需解出集合A和B，在进行集合运算即可．

解答：解：阴影部分为?_UA∩B，
∵A={x||x|≤1，x∈Z}={x|-1≤x≤1}，?_UA={x|x＞1或x＜-1}，
B={x|x²-2x=0}={0，2}
∴?_UA∩B={2}，
故选B．

点评：本题考查的知识点是Venn图表达集合的关系及运算，其中正确理解阴影部分元素满足的性质是解答本题的关键．