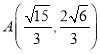题目内容
【题目】在平面直角坐标系xOy中,已知定点F(1,0),点A在x轴的非正半轴上运动,点B在y轴上运动,满足![]() 0,A关于点B的对称点为M,设点M的轨迹为曲线C.
0,A关于点B的对称点为M,设点M的轨迹为曲线C.
(1)求C的方程;
(2)已知点G(3,﹣2),动直线x=t(t>3)与C相交于P,Q两点,求过G,P,Q三点的圆在直线y=﹣2上截得的弦长的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设A(a,0),B(0,b),M(x,y),运用向量的数量积的坐标表示和中点坐标公式,结合代入法,化简可得所求曲线C的方程;
(2)设P(t,2![]() ),Q(t,﹣2
),Q(t,﹣2![]() ),设E(m,0),由|EG|=|EP|,运用两点的距离公式,求得圆E的方程,再令y=﹣2,求得圆在直线y=﹣2上截得的弦长,结合基本不等式,即可得到所求最小值.
),设E(m,0),由|EG|=|EP|,运用两点的距离公式,求得圆E的方程,再令y=﹣2,求得圆在直线y=﹣2上截得的弦长,结合基本不等式,即可得到所求最小值.
(1)设A(a,0),B(0,b),M(x,y),
由点F(1,0),![]()
![]() 0,所以
0,所以![]() ,
,
又B为AM的中点,
所以![]() 0,
0,![]() b,所以a=﹣x,
b,所以a=﹣x,
将![]() 代入
代入![]() 可得
可得![]()
所以C的方程为![]() ;
;
(2)由(1)可得抛物线C的方程为![]() ,令x=t,可得
,令x=t,可得![]() ,
,
设P(t,2![]() ),Q(t,﹣2
),Q(t,﹣2![]() ),由P,Q关于x轴对称,
),由P,Q关于x轴对称,
所以过G,P,Q三点的圆E的圆心在x轴上,
设E(m,0),由|EG|=|EP|,G(3,﹣2),
可得![]() ,
,
化简整理可得m![]() ,
,
圆E的方程为![]()
令y=﹣2,可得![]()
所以圆E在直线y=﹣2上截得的弦长为

又因为![]() 且
且![]()
所以![]() ,
,
所以![]() ,
,
当且仅当![]() 即
即![]() 时取得等号.
时取得等号.
所以当t=3+2![]() 时,圆E在直线y=﹣2上截得的弦长的最小值为4+4
时,圆E在直线y=﹣2上截得的弦长的最小值为4+4![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目