ЬтФПФкШн
ЁОЬтФПЁПЫцзХЯжДњЕчзгММЪѕЕФбИУЭЗЂеЙЃЌЙигкдЊМўКЭЯЕЭГПЩППадЕФбаОПвбЗЂеЙГЩЮЊвЛУХаТЕФбЇПЦЁЊЁЊПЩППадРэТлЃЎдкПЩППадРэТлжаЃЌвЛИідЊМўе§ГЃЙЄзїЕФИХТЪГЦЮЊИУдЊМўЕФПЩППадЃЎдЊМўзщГЩЯЕЭГЃЌЯЕЭГе§ГЃЙЄзїЕФИХТЪГЦЮЊИУЯЕЭГЕФПЩППадЃЎЯжга![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉжжЕчзгдЊМўЃЌУПжж2ИіЃЌУПИідЊМўЕФПЩППадОљЮЊ
ЃЉжжЕчзгдЊМўЃЌУПжж2ИіЃЌУПИідЊМўЕФПЩППадОљЮЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЎЕБФГдЊМўВЛФме§ГЃЙЄзїЪБЃЌИУдЊМўдкЕчТЗжаНЋаЮГЩЖЯТЗЃЎЯжвЊгУет
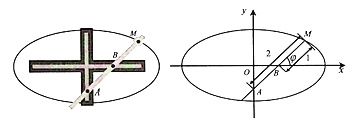
ЃЉЃЎЕБФГдЊМўВЛФме§ГЃЙЄзїЪБЃЌИУдЊМўдкЕчТЗжаНЋаЮГЩЖЯТЗЃЎЯжвЊгУет![]() ИідЊМўзщГЩвЛИіЕчТЗЯЕЭГЃЌгаШчЯТСНжжСЌНгЗНАИПЩЙЉбЁдёЃЌЕБЧвНіЕБДгAЕНBЕФЕчТЗЮЊЭЈТЗзДЬЌЪБЃЌЯЕЭГе§ГЃЙЄзїЃЎ
ИідЊМўзщГЩвЛИіЕчТЗЯЕЭГЃЌгаШчЯТСНжжСЌНгЗНАИПЩЙЉбЁдёЃЌЕБЧвНіЕБДгAЕНBЕФЕчТЗЮЊЭЈТЗзДЬЌЪБЃЌЯЕЭГе§ГЃЙЄзїЃЎ
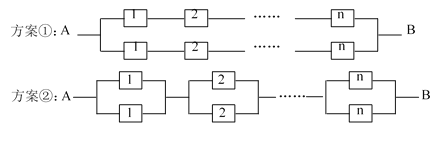
ЃЈ1ЃЉЃЈiЃЉЗжБ№аДГіАДЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЁЂ
ЁЂ![]() ЃЈгУ
ЃЈгУ![]() КЭ
КЭ![]() БэЪОЃЉЃЛ
БэЪОЃЉЃЛ
ЃЈiiЃЉБШНЯ![]() гы
гы![]() ЕФДѓаЁЃЌЫЕУїФФжжСЌНгЗНАИИќЮШЖЈПЩППЃЛ
ЕФДѓаЁЃЌЫЕУїФФжжСЌНгЗНАИИќЮШЖЈПЩППЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌвбжЊАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЃЌМЧДЫЪБЯЕЭГжаЫ№ЛЕЕФдЊМўИіЪ§ЮЊ
ЃЌвбжЊАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЃЌМЧДЫЪБЯЕЭГжаЫ№ЛЕЕФдЊМўИіЪ§ЮЊ![]() ЃЌЧѓЫцЛњБфСП
ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈiЃЉ![]() ЃЌ
ЃЌ![]() ЃЈiiЃЉ
ЃЈiiЃЉ![]() ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎЃЈ2ЃЉМћНтЮіЃЌ
ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎЃЈ2ЃЉМћНтЮіЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЃЈiЃЉРћгУЖдСЂЪТМўЕФИХТЪЙЋЪНМЦЫуЃЌ![]() ИідЊМўДЎСЊЭЈТЗЕФИХТЪЪЧ
ИідЊМўДЎСЊЭЈТЗЕФИХТЪЪЧ![]() ЃЌЖј
ЃЌЖј![]() ИідЊМўВЂСЊЪБВЛЭЈЕФИХТЪЪЧ
ИідЊМўВЂСЊЪБВЛЭЈЕФИХТЪЪЧ![]() ЃЌгЩДЫПЩМЦЫуПЩМЦЫуЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад
ЃЌгЩДЫПЩМЦЫуПЩМЦЫуЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЁЂ
ЁЂ![]() ЃЛЃЈiiЃЉзїВюКѓЙЙдьКЏЪ§
ЃЛЃЈiiЃЉзїВюКѓЙЙдьКЏЪ§![]() ЃЌРћгУЕМЪ§ПЩЕУЦфЕЅЕїадДгЖјЕУ
ЃЌРћгУЕМЪ§ПЩЕУЦфЕЅЕїадДгЖјЕУ![]() гы
гы![]() ЕФДѓаЁЃЌЕУГіНсТлЃЛ
ЕФДѓаЁЃЌЕУГіНсТлЃЛ
ЃЈ2ЃЉдкЗНАИЂкЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЕФЬѕМўЯТЃЌдЊМўЫ№ЛЕЕФИХТЪЪЧЬѕМўИХТЪЃЌПЩМЦЫуБрКХЯрЭЌЕФСНИіВЂСЊдЊМўжажСЖргавЛИіЫ№ЛЕЃЌЧвгавЛИіЫ№ЛЕЕФЬѕМўИХТЪЮЊ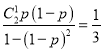 ЃЌгЩДЫПЩжЊЃЌ
ЃЌгЩДЫПЩжЊЃЌ![]() ЃЌвРДЮМЦЫуГіИїИХТЪЃЌЕУЗжВМСаЃЌдйгЩЖўЯюЗжВММЦЫуГіЦкЭћЃЎ
ЃЌвРДЮМЦЫуГіИїИХТЪЃЌЕУЗжВМСаЃЌдйгЩЖўЯюЗжВММЦЫуГіЦкЭћЃЎ
НтЃКЃЈ1ЃЉЃЈiЃЉАДЗНАИЂйНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЃЛ
ЃЛ
АДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППадЮЊ![]() ЃЛ
ЃЛ
ЃЈiiЃЉ![]() ЃЎ
ЃЎ
Сю![]() ЃЌ
ЃЌ![]() Чв
Чв![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌДгЖј
ЃЌДгЖј![]() ЃЌЫљвд
ЃЌЫљвд![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЛ
ЩЯЕЅЕїЕндіЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ЫљвдЃЌ![]() ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎ
ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎ
ЃЈ2ЃЉдкЗНАИЂкЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЕФЬѕМўЯТЃЌБрКХЯрЭЌЕФСНИіВЂСЊдЊМўжажСЖргавЛИіЫ№ЛЕЃЌЧвгавЛИіЫ№ЛЕЕФЬѕМўИХТЪЮЊ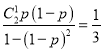 ЃЌгЩДЫПЩжЊЃЌ
ЃЌгЩДЫПЩжЊЃЌ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЫљвдЃЌЫцЛњБфСП![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() ЃЎ
ЃЎ