题目内容
我们知道等比数列与等差数列在许多地方都有类似的性质,请由等差数列{an}的前n项和公式Sn=na1+
d(d为公差),类比地得到等比数列{bn}的前n项积公式Tn=______(q为公比)
| n(n-1) |
| 2 |
在等差数列{an}的前n项和为Sn=na1+
d,
因为等差数列中的求和类比等比数列中的乘积,
所以各项均为正的等比数列{bn}的前n项和Tn=b
•q
故答案为:Tn=b
•q
| n(n-1) |
| 2 |
因为等差数列中的求和类比等比数列中的乘积,
所以各项均为正的等比数列{bn}的前n项和Tn=b
| n1 |
| n(n-1) |
| 2 |
故答案为:Tn=b
| n1 |
| n(n-1) |
| 2 |

练习册系列答案
相关题目
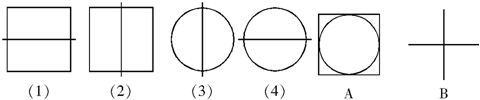
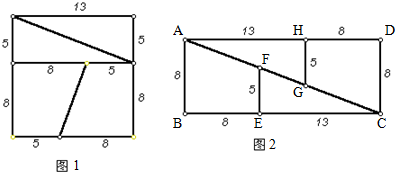
 _______
_______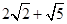 .
.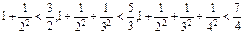 ,…,则可归纳出式子为( )
,…,则可归纳出式子为( )


