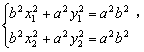题目内容

中心在坐标原点的椭圆上有三个不同的点A、B、C，其中B点的横坐标为4，它们到焦点F（4，0）的距离| AF |，| BF |，| CF |成等差数列，记线段AC的垂直平分线与x轴的交点为T，若直线BT的斜率为，求此椭圆的方程．

 

答案：
解析：

解：如右图，设A（x1，y1），C（x2，y2），

所求椭圆为由统一定义

| AF | = a－ex1，| BF | = a－4e，

| CF | = a－ex2．

∵ 2| BF | = | AF | + | CF |，

∴ 2a－8e = 2a－e ( x1 + x2 )，

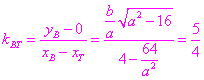
∴ x1 + x2 = 8，设AC中点，

∴ AC的垂直平分线方程为

T点横坐标为 ①

由  ．  ②

由①，②

．

又 ，

∴ a = 5，b2 = 25－16 = 9．

所求椭圆方程为 ． 

 


提示：

 


练习册系列答案
相关题目
设中心在坐标原点的椭圆M与双曲线2x2-2y2=1有公共焦点，且它们的离心率互为倒数
（Ⅰ）求椭圆M的方程；
（Ⅱ）过点A（2，0）的直线交椭圆M于P、Q两点，且满足OP⊥OQ，求直线PQ的方程．
已知焦点在x轴上，中心在坐标原点的椭圆C的离心率为
4
5
，且过点（
10
2
3
，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线l分别切椭圆C与圆M：x2+y2=R2（其中3＜R＜5）于A、B两点，求|AB|的最大值．
已知中心在坐标原点的椭圆经过直线x-2y-4=0与坐标轴的两个交点，则该椭圆的离心率为
 
．
已知焦点在x轴上，中心在坐标原点的椭圆C的离心率为
4
5
，且过点P(
10
2
3
，1)
（1）求椭圆C的标准方程
（2）直线l：y=kx+m分别切椭圆C与圆M：x2+y2=15于A、B两点，求|AB|的值．
已知焦点在x轴上，中心在坐标原点的椭圆C的离心率为
4
5
，且过点(
10
2
3
，1)，求椭圆C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网