题目内容
7.已知函数$f(x)=3sin(\frac{x}{2}+\frac{π}{6})+3$(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)若f(2α)-3=$\sqrt{2}$,求$cos(\frac{π}{3}-α)$.
分析 (1)利用五点法即可画出它在一个周期内的闭区间上的图象;
(2)根据条件进行化简,结合同角的三角函数关系进行化简即可.
解答 解:(1)列表
| x | $-\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{x}{2}$+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | 2π | 2π | 2π |
| y | 3 | 6 | 3 | 0 | 3 |
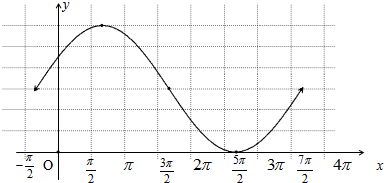 …(8分)
…(8分)(2)∵$f(2α)-3=3sin(α+\frac{π}{6})=\sqrt{2}$,
∴$sin(α+\frac{π}{6})=\frac{{\sqrt{2}}}{3}$,
∴$cos(\frac{π}{3}-α)=sin(α+\frac{π}{6})=\frac{{\sqrt{2}}}{3}$…(12分)
点评 本题主要考查三角函数图象和三角函数值的化简,利用五点法是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
15.方程mx2+ny2=1不可能表示的曲线为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
12.观察下列顺序排列的等式:9×0+1=1;9×1+2=11;9×2+3=21;9×3+4=31…猜想第n个等式应为( )
| A. | 9(n+1)+n=10n+9 | B. | 9(n-1)+(n-1)=10n-10 | C. | 9n+(n-1)=10n-1 | D. | 9(n-1)+n=10n-9 |
19.如果点M(sinθ,cosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.2014年国家加大对科技创新行业的支持力度,某研究机构对一新型行业的企业年投入x(单位:万元)与年盈利y(单位:万元)情况进行了统计分析,得下表数据:
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a中的b的值为0.7,若某企业计划年投资14万元,则该企业的年盈利约为( )
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 6.5 | B. | 7 | C. | 7.5 | D. | 8 |
17.复数$z=3i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
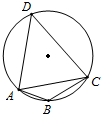 在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:
在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求: