题目内容
【题目】已知![]() 都是定义域为
都是定义域为![]() 的连续函数.已知:
的连续函数.已知:![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②
恒成立;②![]() 都有
都有![]() .
.![]() 满足:①
满足:①![]() 都有
都有![]() ;②当
;②当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据条件可得函数g(x)的奇偶性和单调性,利用条件可得函数f(x)的周期性,将不等式进行转化为求函数最值恒成立即可得到结论.
∵函数g(x)满足:当x>0时,g'(x)>0恒成立且对任意x∈R都有g(x)=g(﹣x),
∴函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),
∴g[f(x)]≤g(a2﹣a+2),x∈![]() 恒成立|f(x)|≤|a2﹣a+2|恒成立,只要使得定义域内|f(x)|max≤|a2﹣a+2|min,
恒成立|f(x)|≤|a2﹣a+2|恒成立,只要使得定义域内|f(x)|max≤|a2﹣a+2|min,
由f(x+![]() )=f(x﹣
)=f(x﹣![]() ),得f(x+2
),得f(x+2![]() )=f(x),
)=f(x),
即函数f(x)的周期T=2![]() ,
,
∵x∈[﹣![]() ,
,![]() ]时,f(x)=x3﹣3x,
]时,f(x)=x3﹣3x,
求导得:f′(x)=3x2﹣3=3(x+1)(x﹣1),该函数过点(﹣![]() ,0),(0,0),(
,0),(0,0),(![]() ,0),
,0),
且函数在x=﹣1处取得极大值f(﹣1)=2,
在x=1处取得极小值f(1)=﹣2,
即函数f(x)在R上的最大值为2,
∵x∈![]() ,函数的周期是2
,函数的周期是2![]() ,
,
∴当x∈![]() 时,函数f(x)的最大值为2,
时,函数f(x)的最大值为2,
由2≤|a2﹣a+2|,即2≤a2﹣a+2,
则a2﹣a≥0,
解得:a≥1或a≤0.
故答案为:D

【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如列联表.
的概率分布如列联表.
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响求该企业在这两个月内共被消费者投诉![]() 次的概率.
次的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
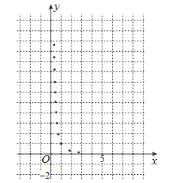
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为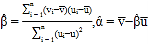 .
.