题目内容
(本小题满分14分)
如图,四棱锥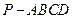 中,
中, 平面
平面 ,底面
,底面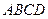 为矩形,
为矩形,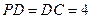 ,
,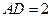 ,
,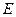 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)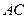 边上是否存在一点
边上是否存在一点 ,使得
,使得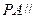 平面
平面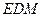 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.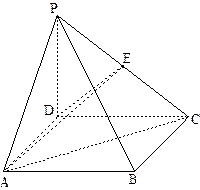
如图,四棱锥
 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形,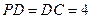 ,
,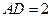 ,
,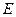 为
为 的中点.
的中点.(Ⅰ)求证:
 ;
;(Ⅱ)求三棱锥
 的体积;
的体积;(Ⅲ)
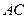 边上是否存在一点
边上是否存在一点 ,使得
,使得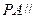 平面
平面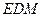 ,若存在,求出
,若存在,求出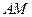 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.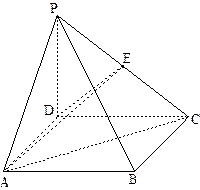
(1)略(2) (3)
(3)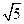
 (3)
(3)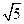
(Ⅰ)证明:因为 平面
平面 ,
,
所以 .………………………………………………………………2分
.………………………………………………………………2分
又因为 是矩形,
是矩形,
所以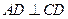 .………………………………………………………………3分
.………………………………………………………………3分
因为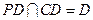 ,
,
所以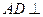 平面
平面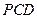 .
.
又因为
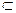 平面
平面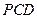 ,
,
所以 .………………………………………………………………5分
.………………………………………………………………5分
(Ⅱ)解:因为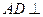 平面
平面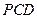 ,
,
所以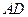 是三棱锥
是三棱锥 的高.
的高.
因为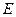 为
为 的中点,且
的中点,且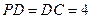 ,
,
 所以
所以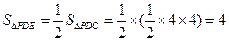 .………………………………………7分
.………………………………………7分
又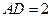 ,
,
所以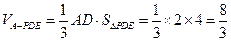 .………9分
.………9分
(Ⅲ)取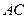 中点
中点 ,连结
,连结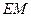 ,
,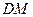 ,
,
因为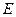 为
为 的中点,
的中点, 是
是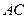 的中点,
的中点,
所以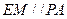 .
.
又因为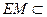 平面
平面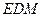 ,
,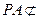 平面
平面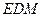 ,
,
所以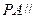 平面
平面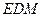 .…………………………………………………12分
.…………………………………………………12分
所以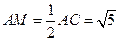 .
.
即在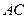 边上存在一点
边上存在一点 ,使得
,使得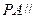 平面
平面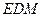 ,
,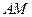 的长为
的长为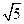 .…14分
.…14分
 平面
平面 ,
,所以
 .………………………………………………………………2分
.………………………………………………………………2分又因为
 是矩形,
是矩形,所以
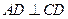 .………………………………………………………………3分
.………………………………………………………………3分因为
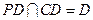 ,
,所以
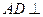 平面
平面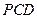 .
.又因为

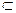 平面
平面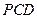 ,
,所以
 .………………………………………………………………5分
.………………………………………………………………5分(Ⅱ)解:因为
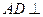 平面
平面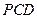 ,
,所以
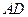 是三棱锥
是三棱锥 的高.
的高.因为
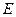 为
为 的中点,且
的中点,且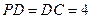 ,
, 所以
所以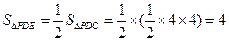 .………………………………………7分
.………………………………………7分又
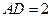 ,
,所以
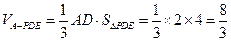 .………9分
.………9分(Ⅲ)取
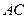 中点
中点 ,连结
,连结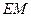 ,
,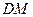 ,
,因为
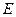 为
为 的中点,
的中点, 是
是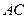 的中点,
的中点,所以
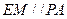 .
. 又因为
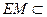 平面
平面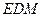 ,
,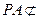 平面
平面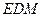 ,
,所以
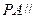 平面
平面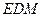 .…………………………………………………12分
.…………………………………………………12分所以
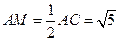 .
.即在
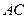 边上存在一点
边上存在一点 ,使得
,使得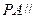 平面
平面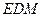 ,
,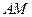 的长为
的长为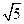 .…14分
.…14分
练习册系列答案
相关题目
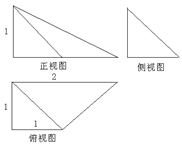
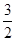

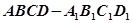 中,过顶点
中,过顶点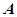 任作一条直线
任作一条直线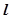 ,与异面直线
,与异面直线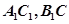
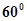 ,则这样的直线
,则这样的直线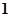 条
条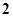 条
条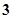 条
条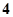 条
条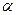 .条件“直线l与平面
.条件“直线l与平面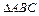 中,AB=2,BC=1,
中,AB=2,BC=1,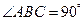 ,平面ABC外一点
,平面ABC外一点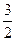 ,则三棱锥P—ABC的体积是( )
,则三棱锥P—ABC的体积是( )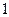
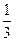
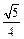
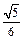
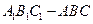 中,
中, ,
, ,点G与E分别为线段
,点G与E分别为线段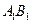 和
和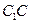 的中点,点D与F分别为线段AC和AB上的动点。若
的中点,点D与F分别为线段AC和AB上的动点。若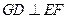 ,则线段DF长度的最小值是( )
,则线段DF长度的最小值是( )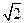
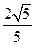
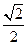
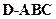 的外接球的球心O满足
的外接球的球心O满足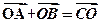 ,且外接球的体积为
,且外接球的体积为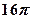 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 .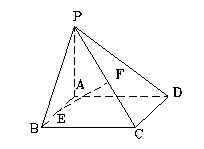 (1)求证:
(1)求证: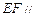 平面PAD;
平面PAD;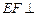 平面PCD.
平面PCD.