题目内容
16.在同一坐标系中,将曲线y=2sin3x变为曲线y=sinx的伸缩变换是( )| A. | $\left\{{\begin{array}{l}{x=3{x^/}}\\{y=\frac{1}{2}{y^/}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{{x^/}=3x}\\{{y^/}=\frac{1}{2}y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=3{x^/}}\\{y=2{y^/}}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{{x^/}=3x}\\{{y^/}=2y}\end{array}}\right.$ |
分析 将曲线y=2sin3x变为曲线y=sinx(写成:y′=sinx′),横坐标变为原来的3倍,纵坐标变为原来的$\frac{1}{2}$倍,故可得伸缩变换.
解答 解:将曲线y=2sin3x变为曲线y=sinx即y′=sinx′,
横坐标变为原来的3倍,纵坐标变为原来的$\frac{1}{2}$倍,
将曲线y=2sin3x变为曲线y=sinx的伸缩变换是:$\left\{{\begin{array}{l}{{x^/}=3x}\\{{y^/}=\frac{1}{2}y}\end{array}}\right.$,
故选B.
点评 本题主要考查了伸缩变换的有关知识,以及图象之间的联系,主要考查函数y=Asin(ωx+∅)的图象变换,判断横坐标变为原来的3倍,纵坐标变为原来的$\frac{1}{2}$倍,是解题的关键.属于基础题.

练习册系列答案
相关题目
8.复数z=$\frac{1-2i}{3+4i}$(i为虚数单位)的实部为( )
| A. | -$\frac{2}{5}$ | B. | -1 | C. | -$\frac{1}{5}$ | D. | $\frac{11}{25}$ |
6.已知y=f(x)对任意x有f(-x)=f(x),f(x)=-f(x+1),且在[0,1]上为减函数,则( )
| A. | f($\frac{7}{5}$)<f($\frac{7}{2}$)<f($\frac{7}{3}$) | B. | f($\frac{7}{2}$)<f($\frac{7}{3}$)<f($\frac{7}{5}$) | C. | f($\frac{7}{3}$)<f($\frac{7}{2}$)<f($\frac{7}{5}$) | D. | f($\frac{7}{5}$)<f($\frac{7}{3}$)<f($\frac{7}{2}$) |
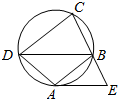 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则DC=$\frac{25}{4}$.