题目内容
(2012•济南三模)下面给出的四个命题中:
①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为(x-1)2+y2=1;
②若m=-2,则直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直;
③命题“?x∈R,使得x2+3x+4=0”的否定是“?x∈R,都有x2+3x+4≠0”;
④将函数y=sin2x的图象向右平移
个单位,得到函数y=sin(2x-
)的图象.
其中是真命题的有
①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为(x-1)2+y2=1;
②若m=-2,则直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直;
③命题“?x∈R,使得x2+3x+4=0”的否定是“?x∈R,都有x2+3x+4≠0”;
④将函数y=sin2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
其中是真命题的有
①②③
①②③
(将你认为正确的序号都填上).分析:①先求抛物线是焦点为(1,0),可求圆的半径为r=1,从而可求圆的方程
②把m=-2代入两直线方程即可检验直线是否垂直
③根据特称命题的否定是全称命题可知正确;
④函数向右平移
,得到的函数为y=sin2(x-
)=sin(2x-
)即可判断
②把m=-2代入两直线方程即可检验直线是否垂直
③根据特称命题的否定是全称命题可知正确;
④函数向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解答:解:①抛物线是焦点为(1,0),圆的半径为r=1,所以圆的方程为(x-1)2+y2=1,正确;
②当m=-2,两直线方程为y=
和x=-
,两直线垂直所以正确;
③根据特称命题的否定是全称命题可知正确;
④函数向右平移
,得到的函数为y=sin2(x-
)=sin(2x-
),所以不正确.
所以正确的命题有①②③.
故答案为:①②③
②当m=-2,两直线方程为y=
| 1 |
| 2 |
| 3 |
| 4 |
③根据特称命题的否定是全称命题可知正确;
④函数向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
所以正确的命题有①②③.
故答案为:①②③
点评:本题主要考查了圆的标准方程的求解,直线垂直的条件的应用,命题的否定及函数的图象的平移等知识的综合应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
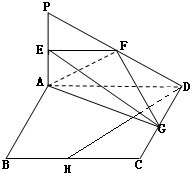 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.