题目内容
试问: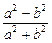 与
与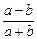 (a、b<0)的大小关系,并说明理由.
(a、b<0)的大小关系,并说明理由.
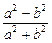 与
与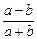 (a、b<0)的大小关系,并说明理由.
(a、b<0)的大小关系,并说明理由.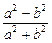 -
-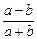
=
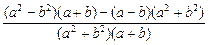
=
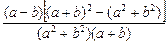
=
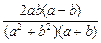 .
.由于a<0,b<0,∴ab>0,a+b<0,a2>0,b2>0.
∴a2+b2>0并且有2ab>0.
则(a2+b2)(a+b)<0.
要判断
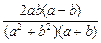 与0的关系,需对a-b与0的关系分类:
与0的关系,需对a-b与0的关系分类:(1)若0>a>b,则a-b>0,则2ab(a-b)>0,于是
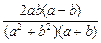 <0.
<0.此时,
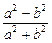 <
<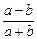 .
.(2)若0>b>a,则a-b<0,则2ab(a-b)<0,于是
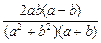 >0.
>0.此时,
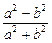 >
>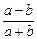 .
.(3)若0>a=b,则a-b=0,则2ab(a-b)=0,于是
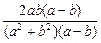 =0.
=0.此时,
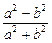 =
= 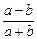 .
.两个数(或式)进行大小比较时,通常用作差法,它的一般步骤是:(1)作差;(2)变形;(3)定号.
作差的依据是:实数大小顺序与实数运算性质间的关系,即a>b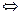 a-b>0;a=b
a-b>0;a=b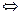 a-b=0;a<b
a-b=0;a<b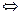 a-b<0.
a-b<0.
变形的方法是:采用配方法、因式分解法将差式化为若干个因式连乘积的形式或完全平方式的和的形式.
定号:由各因式的符号判断差的符号.
此题在判断符号时,要分类讨论.分类讨论是重要的数学思想,要知道为什么分类,怎样分类.分类时,要做到不重不漏.
作差的依据是:实数大小顺序与实数运算性质间的关系,即a>b
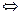 a-b>0;a=b
a-b>0;a=b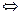 a-b=0;a<b
a-b=0;a<b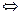 a-b<0.
a-b<0.变形的方法是:采用配方法、因式分解法将差式化为若干个因式连乘积的形式或完全平方式的和的形式.
定号:由各因式的符号判断差的符号.
此题在判断符号时,要分类讨论.分类讨论是重要的数学思想,要知道为什么分类,怎样分类.分类时,要做到不重不漏.

练习册系列答案
相关题目
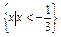 ,求关于x的不等式(a-3b)x+(b-2a)>0的解集.
,求关于x的不等式(a-3b)x+(b-2a)>0的解集.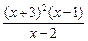 ≤0的解集是
≤0的解集是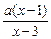 >1(a>0).
>1(a>0).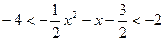
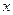 使得不等式|
使得不等式| 成立,则实数
成立,则实数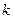 的取值范围是 。
的取值范围是 。