题目内容
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() ,以原点
,以原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(1)若曲线C1方程中的参数是α,且C1与C2有且只有一个公共点,求C1的普通方程;
(2)已知点A(0,1),若曲线C1方程中的参数是t,0<α<π,且C1与C2相交于P,Q两个不同点,求![]() 的最大值.
的最大值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)利用公式直接把极坐标方程化为直角坐标方程,利用圆与圆相切,可以得到等式,求出![]() ,进而得到结果;
,进而得到结果;
(2)把曲线![]() 参数方程代入曲线
参数方程代入曲线![]() 直角坐标方程,得到一个一元二次方程,设交点
直角坐标方程,得到一个一元二次方程,设交点![]() 对应的参数分别是
对应的参数分别是![]() ,利用一元二次方程根与系数的关系,求得
,利用一元二次方程根与系数的关系,求得![]() 的表达式,求出最大值.
的表达式,求出最大值.
(1)∵ρ=2cosθ,∴曲线C2的直角坐标方程为∴(x﹣1)2+y2=1,
∵α是曲线C1:![]() 的参数,∴C1的普通方程为x2+(y﹣1)2=t2,
的参数,∴C1的普通方程为x2+(y﹣1)2=t2,
∵C1与C2有且只有一个公共点,∴|t|![]() 1或|t|
1或|t|![]() 1,
1,
∴C1的普通方程为x2+(y﹣1)2=(![]() )2或x2+(y﹣1)2=(
)2或x2+(y﹣1)2=(![]() )2
)2
(2)∵t是曲线C1:![]() 的参数,∴C1是过点A(0,1)的一条直线,
的参数,∴C1是过点A(0,1)的一条直线,
设与点P,Q相对应的参数分别是t1,t2,把![]() ,代入(x﹣1)2+y2=1得t2+2(sinα﹣cosα)t+1=0,∴
,代入(x﹣1)2+y2=1得t2+2(sinα﹣cosα)t+1=0,∴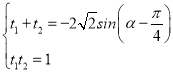
∴![]() |t1|+|t2|=|t1+t2|=2
|t1|+|t2|=|t1+t2|=2![]() |sin(α
|sin(α![]() )|≤2
)|≤2![]() ,
,
当α![]() 时,△=4(sinα﹣cosα)2﹣4=4>0,
时,△=4(sinα﹣cosα)2﹣4=4>0,
![]() 取最大值2
取最大值2![]() .
.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
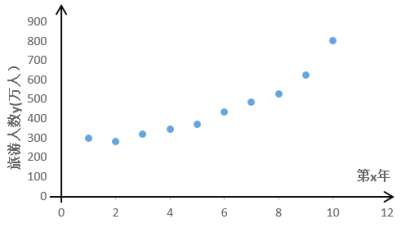
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为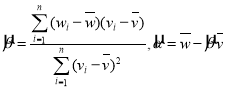 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数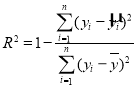 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.