Question

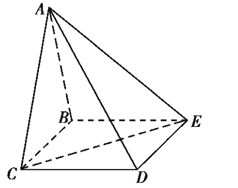
【题目】四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC底面BCDE，BC=2,CD=,AB=AC

（1）证明.

（2）设侧面ABC为等边三角形，求二面角C-AD-E的余弦值。

Answer 1

【答案】(1)见证明；(2)

【解析】

（1）作AO⊥BC，垂足为O，连接OD，利用三垂线定理，即可证得；

（2）利用二面角的定义，得到∠CGE是二面角C-AD-E的平面角，在中，利用余弦定理，即可求解二面角的余弦值.

(1)作AO⊥BC，垂足为O，连接OD，

由题设知，AO⊥底面BCDE，且O为BC中点，

由，可得RtΔOCD∽Rt△CDE，从而∠ODC=∠CED，于是CE⊥OD,

由三垂线定理，可得.

(2)由题意知BE⊥BC，所以BE⊥侧面ABC，又BE侧面ABE，∴侧面ABE⊥侧面ABC.

作CF⊥AB，垂足为F，连接FE,则CF⊥平面ABE，

故∠CEF为CE与平面ABE所成的角，且∠CEF=45°，

由CE=，得CF=，

又∵BC=2，△ABC为等边三角形，

作CG⊥AD，垂足为G，连GE

由(1)知，CE⊥AD,又CE∩CG=C,

故AD⊥平面CGE,AD⊥GE，所以∠CGE是二面角C-AD-E的平面角.

，

，

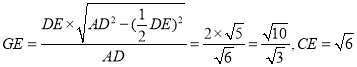在中，由余弦定理得，

所以二面角C-AD-E的余弦值为.