题目内容
已知C为线段AB上一点,P为直线AB外一点,I为PC上一点,满足|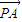 |-|
|-|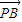 |=4,|
|=4,|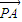 -
-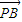 |=10,
|=10,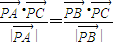 ,且
,且 =
=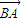 +λ(
+λ(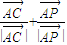 ),(λ>0),则
),(λ>0),则 的值为( )
的值为( )A.2
B.4
C.3
D.5
【答案】分析:根据  表示|
表示|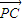 |cos∠APC=|
|cos∠APC=| ||cos∠CPB,即∠APC=∠CPB,且
||cos∠CPB,即∠APC=∠CPB,且 =
= +λ(
+λ( ),(λ>0),表示I在∠BAP的角平分线上,
),(λ>0),表示I在∠BAP的角平分线上,
即I是三角形ABP的内心,余下的问题就比较简单.
解答:解:由| -
-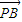 |=10,可得|AB|=10.
|=10,可得|AB|=10.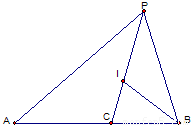
由 ,可得|
,可得| |cos∠APC=|
|cos∠APC=| ||cos∠CPB,即∠APC=∠CPB,即PC为∠APB的角平分线.
||cos∠CPB,即∠APC=∠CPB,即PC为∠APB的角平分线.
由于I为PC上一点, =
= +λ(
+λ( ),(λ>0),表示点I在∠CAP的角平分线上,即I是三角形ABP的内心.
),(λ>0),表示点I在∠CAP的角平分线上,即I是三角形ABP的内心.
而要求的式子 表示的是
表示的是 在
在 上的投影长度.
上的投影长度.
过I做IK垂直于AB于K,则由圆的切线性质和题意可得|AK|-|BK|=4,|AK|+|BK|=10,解得|BK|=3即所求,
故选C.
点评:本题考查向量在几何中的应用,本题解题的关键是正确理解条件中所给的几个关系式,注意把条件转化成我们所熟悉的条件,本题是一个比较好的题目,属于中档题.
 表示|
表示|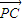 |cos∠APC=|
|cos∠APC=| ||cos∠CPB,即∠APC=∠CPB,且
||cos∠CPB,即∠APC=∠CPB,且 =
= +λ(
+λ( ),(λ>0),表示I在∠BAP的角平分线上,
),(λ>0),表示I在∠BAP的角平分线上,即I是三角形ABP的内心,余下的问题就比较简单.
解答:解:由|
 -
-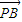 |=10,可得|AB|=10.
|=10,可得|AB|=10.
由
 ,可得|
,可得| |cos∠APC=|
|cos∠APC=| ||cos∠CPB,即∠APC=∠CPB,即PC为∠APB的角平分线.
||cos∠CPB,即∠APC=∠CPB,即PC为∠APB的角平分线.由于I为PC上一点,
 =
= +λ(
+λ( ),(λ>0),表示点I在∠CAP的角平分线上,即I是三角形ABP的内心.
),(λ>0),表示点I在∠CAP的角平分线上,即I是三角形ABP的内心.而要求的式子
 表示的是
表示的是 在
在 上的投影长度.
上的投影长度.过I做IK垂直于AB于K,则由圆的切线性质和题意可得|AK|-|BK|=4,|AK|+|BK|=10,解得|BK|=3即所求,
故选C.
点评:本题考查向量在几何中的应用,本题解题的关键是正确理解条件中所给的几个关系式,注意把条件转化成我们所熟悉的条件,本题是一个比较好的题目,属于中档题.

练习册系列答案
相关题目
 选考题
选考题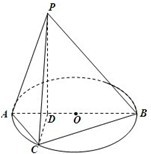 (2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且
(2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且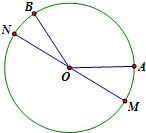 已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在圆内,且满足
已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在圆内,且满足