题目内容
(2013•海淀区一模)已知圆M:(x-
)2+y2=r2(r>0).若椭圆C:
+
=1(a>b>0)的右顶点为圆M的圆心,离心率为
.
(Ⅰ)求椭圆C的方程;
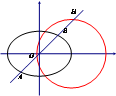
(Ⅱ)若存在直线l:y=kx,使得直线l与椭圆C分别交于A,B两点,与圆M分别交于G,H两点,点G在线段AB上,且|AG|=|BH|,求圆M半径r的取值范围.
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若存在直线l:y=kx,使得直线l与椭圆C分别交于A,B两点,与圆M分别交于G,H两点,点G在线段AB上,且|AG|=|BH|,求圆M半径r的取值范围.
分析:(I)设椭圆的焦距为2c,由椭圆右顶点为圆心可得a值,进而由离心率可得c值,根据平方关系可得b值;
(II)由点G在线段AB上,且|AG|=|BH|及对称性知点H不在线段AB上,所以要使|AG|=|BH|,只要|AB|=|GH|,设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程消掉y得x的二次方程,利用韦达定理及弦长公式可得|AB|,在圆中利用弦心距及勾股定理可得|GH|,根据|AB|=|GH|得r,k的方程,分离出r后按k是否为0进行讨论,借助基本函数的范围即可求得r范围;
(II)由点G在线段AB上,且|AG|=|BH|及对称性知点H不在线段AB上,所以要使|AG|=|BH|,只要|AB|=|GH|,设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程消掉y得x的二次方程,利用韦达定理及弦长公式可得|AB|,在圆中利用弦心距及勾股定理可得|GH|,根据|AB|=|GH|得r,k的方程,分离出r后按k是否为0进行讨论,借助基本函数的范围即可求得r范围;
解答:解:(I)设椭圆的焦距为2c,
由椭圆右顶点为圆M的圆心(
,0),得a=
,
又
=
,所以c=1,b=1.
所以椭圆C的方程为:
+y2=1.
(II)设A(x1,y1),B(x2,y2),
由直线l与椭圆C交于两点A,B,则
,
所以(1+2k2)x2-2=0,则x1+x2=0,x1x2=-
,
所以|AB|=
=
,
点M(
,0)到直线l的距离d=
,
则|GH|=2
,
显然,若点H也在线段AB上,则由对称性可知,直线y=kx就是y轴,矛盾,
所以要使|AG|=|BH|,只要|AB|=|GH|,
所以
=4(r2-
),
r2=
+
=
=2(1+
),
当k=0时,r=
,
当k≠0时,r2=2(1+
)<2(1+
)=3,
又显然r2=2(1+
)>2,所以
<r<
,
综上,
≤r<
.
由椭圆右顶点为圆M的圆心(
| 2 |
| 2 |
又
| c |
| a |
| ||
| 2 |
所以椭圆C的方程为:
| x2 |
| 2 |
(II)设A(x1,y1),B(x2,y2),
由直线l与椭圆C交于两点A,B,则
|
所以(1+2k2)x2-2=0,则x1+x2=0,x1x2=-
| 2 |
| 1+2k2 |
所以|AB|=
(1+k2)
|
|
点M(
| 2 |
|
| ||
|
则|GH|=2
r2-
|
显然,若点H也在线段AB上,则由对称性可知,直线y=kx就是y轴,矛盾,

所以要使|AG|=|BH|,只要|AB|=|GH|,
所以
| 8(1+k2) |
| 1+2k2 |
| 2k2 |
| 1+k2 |
r2=
| 2k2 |
| 1+k2 |
| 2(1+k2) |
| 1+2k2 |
| 2(3k4+3k2+1) |
| 2k4+3k2+1 |
| k4 |
| 2k4+3k2+1 |
当k=0时,r=
| 2 |
当k≠0时,r2=2(1+
| 1 | ||||
|
| 1 |
| 2 |
又显然r2=2(1+
| 1 | ||||
|
| 2 |
| 3 |
综上,
| 2 |
| 3 |
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分类讨论思想,考查学生分析问题解决问题的能力,弦长公式、韦达定理是解决该类问题的基础知识,要熟练掌握.

练习册系列答案
相关题目
 (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN= (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且