题目内容
 选考题
选考题请从下列三道题当中任选一题作答,如果多做,则按所做的第一题计分,请在答题卷上注明题号.
22-1设函数f(x)=|2x-1|+|2x-3|
(1)解不等式f(x)≤5x+1;
(2)若g(x)=
| 1 | ||
|
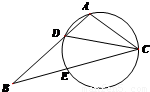
22-2如图,在△ABC中,CD是∠ACB的角平分线,△ACD的外接圆交BC于E,AB=2AC,
(1)求证:BE=2AD;
(2)当AC=1,BC=2时,求AD的长.
22-3已知P为半圆C:
|
| π |
| 3 |
(1)求以O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(2)求直线AM的参数方程.
分析:22-1(1)原不等式等价于
或
或
解之即可;
(2)依题意,f(x)+m=0在R上无解,可求得f(x)min,令-m=f(x)<f(x)min即可.
22-2:(1)连接DE,由△BDE∽△BCA可证得结论;
(2)设AD=t,根据割线定理得 BD•BA=BE•BC,整理得(2-t)•2=2t•2,从而解得答案;
23-3:(1)由已知,点M的极角为
,极径等于
,从而可求得点M的极坐标;
(2)由点M的直角坐标为(
,
),A(1,0,即可求得直线AM的参数方程.
|
|
|
(2)依题意,f(x)+m=0在R上无解,可求得f(x)min,令-m=f(x)<f(x)min即可.
22-2:(1)连接DE,由△BDE∽△BCA可证得结论;
(2)设AD=t,根据割线定理得 BD•BA=BE•BC,整理得(2-t)•2=2t•2,从而解得答案;
23-3:(1)由已知,点M的极角为
| π |
| 3 |
| π |
| 3 |
(2)由点M的直角坐标为(
| π |
| 6 |
| ||
| 6 |
解答:22-1 解:(1)原不等式等价于:于
或
或
,
因此不等式的解集为{x|x≥
}.
(2)由于g(x)=
的定义域为R
∴f(x)+m=0在R上无解
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2即f(x)min=2
∴-m<2,即m>-2
22-2证明:(1)连接DE,
∵ACDE为圆的内接四边形.
∴∠BDE=∠BCA,
又∠DBE=∠CBA,
∴△BDE∽△BCA 即
=
,
而 AB=2AC,
∴BE=2DE.
又CD是∠ACB的平分线,
∴AD=DE 从而BE=2AD.
(2)由条件得 AB=2AC=2
设AD=t,根据割线定理得 BD•BA=BE•BC,即(AB-AD)•BA=2AD•2
∴(2-t)•2=2t•2,解得t=
,即AD=
.
22-3解:(1)由已知,点M的极角为
,极径等于
,所以M(
,
).
(2)点M的直角坐标为(
,
),A(1,0),故直线AM的参数方程为
(t为参数).
|
|
|
因此不等式的解集为{x|x≥
| 1 |
| 3 |
(2)由于g(x)=
| 1 | ||
|
∴f(x)+m=0在R上无解
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2即f(x)min=2
∴-m<2,即m>-2
22-2证明:(1)连接DE,
∵ACDE为圆的内接四边形.
∴∠BDE=∠BCA,
又∠DBE=∠CBA,
∴△BDE∽△BCA 即
| BE |
| BA |
| DE |
| CA |
而 AB=2AC,
∴BE=2DE.
又CD是∠ACB的平分线,
∴AD=DE 从而BE=2AD.
(2)由条件得 AB=2AC=2
设AD=t,根据割线定理得 BD•BA=BE•BC,即(AB-AD)•BA=2AD•2
∴(2-t)•2=2t•2,解得t=
| 2 |
| 3 |
| 2 |
| 3 |
22-3解:(1)由已知,点M的极角为
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(2)点M的直角坐标为(
| π |
| 6 |
| ||
| 6 |
|
点评:本题考查绝对值不等式的解法,考查与圆有关的比例线段,考查点的极坐标和直角坐标的互化,综合性强,难度大,属于难题.

练习册系列答案
相关题目
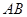 是⊙
是⊙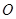 的直径,
的直径,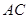 是弦,∠BAC的平分线
是弦,∠BAC的平分线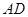 交⊙
交⊙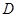 ,
,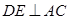 交
交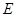 ,
,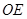 交
交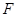 .
.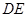 是⊙
是⊙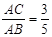 ,求
,求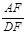 的值.
的值.
 定义域为R,求实数m的取值范围.
定义域为R,求实数m的取值范围. 上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为
上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为