题目内容
【题目】已知函数f(x)=(m﹣1)x2+3x﹣2m,(m∈R).
(1)解关于x的不等式f(x)+x2﹣1<4x﹣m;
(2)若f(x)<0的解集为(﹣4,1),g(x)=f(x)﹣x+5,对于n∈N*,证明:![]() .
.
【答案】(1) 当m>0,不等式的解集为(﹣1,1![]() ),当m=0时,不等式的解集为(﹣1,+∞),当
),当m=0时,不等式的解集为(﹣1,+∞),当![]() m<0,不等式的解集为(﹣∞,1
m<0,不等式的解集为(﹣∞,1![]() )∪(﹣1,+∞),当m
)∪(﹣1,+∞),当m![]() 时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),当m
时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),当m![]() ,不等式的解集为(﹣∞,﹣1)∪(1
,不等式的解集为(﹣∞,﹣1)∪(1![]() ,+∞);(2)证明见详解.
,+∞);(2)证明见详解.
【解析】
(1)整理不等式,分解因式,对参数进行分类讨论,即可求得解集;
(2)由不等式的解集求得参数![]() 的值,再利用放缩的方法,证明不等式即可.
的值,再利用放缩的方法,证明不等式即可.
(1)f(x)=(m﹣1)x2+3x﹣2m,
f(x)+x2﹣1<4x﹣m,
∴(m﹣1)x2+3x﹣2m+x2﹣1<4x﹣m,
即mx2﹣x﹣(m+1)<0,
即(x+1)[mx﹣(m+1)]<0,
①当m=0时,﹣x﹣1<0,解得x>﹣1,
②当m>0时,原不等式为(x+1)[x﹣(1![]() )]<0,
)]<0,
解得﹣1<x<1![]() ,
,
③当m<0时,原不等式为(x+1)[x﹣(1![]() )]>0,
)]>0,
令(x+1)[x﹣(1![]() )]=0,
)]=0,
解得x=﹣1或x=1![]() ,
,
⒈若﹣1>1![]() ,即
,即![]() m<0,
m<0,
解得x>﹣1或x<1![]() ,
,
⒉若﹣1=1![]() ,即m
,即m![]() ,
,
解得x≠﹣1,
⒊若﹣1<1![]() ,即m
,即m![]() ,
,
解得x<﹣1或x>1![]() ,
,
综上所述:
当m>0,不等式的解集为(﹣1,1![]() ),
),
当m=0时,不等式的解集为(﹣1,+∞),
当![]() m<0,不等式的解集为(﹣∞,1
m<0,不等式的解集为(﹣∞,1![]() )∪(﹣1,+∞),
)∪(﹣1,+∞),
当m![]() 时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),
时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),
当m![]() ,不等式的解集为(﹣∞,﹣1)∪(1
,不等式的解集为(﹣∞,﹣1)∪(1![]() ,+∞)
,+∞)
(2)∵f(x)<0的解集为(﹣4,1),
∴f(x)=(m﹣1)x2+3x﹣2m=0的两个根为﹣4,1
∴﹣4+1![]() ,﹣4×1
,﹣4×1![]() ,
,
解得m=2,
∴f(x)=x2+3x﹣4,
∴g(x)=f(x)﹣x+5=x2+3x﹣4﹣x+5=x2+2x+1=(x+1)2,
∴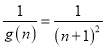 ,
,
要证明![]() ,
,
只要证![]() ,
,
即证 ,
,
①∵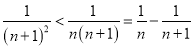 ,
,
∴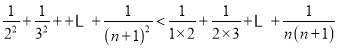
![]() 1
1![]() 1
1![]() ,
,
即证不等式的右边.
②∵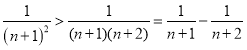 ,
,
∴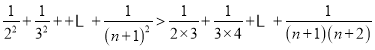
═![]() ,
,
即证不等式的右边.
综上所述:![]() .即证.
.即证.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?