题目内容
若α∈(3π,4π),则
-
等于( )
|
|
分析:根据α的范围求出
的范围,确定出cos
>0,sin
<0,所求式子利用二倍角的余弦函数公式及绝对值的代数意义化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数即可.
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
解答:解:∵α∈(3π,4π),∴
∈(
,2π),
∴cos
>0,sin
<0,
原式=
-
=|cos
|-|sin
|=cos
+sin
=
sin(
+
).
故选B
| α |
| 2 |
| 3π |
| 2 |
∴cos
| α |
| 2 |
| α |
| 2 |
原式=
cos2
|
sin2
|
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| 2 |
| α |
| 2 |
| π |
| 4 |
故选B
点评:此题考查了三角函数的化简求值,涉及的知识有:二倍角的余弦函数公式,两角和与差的正弦函数公式,以及绝对值的代数意义,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
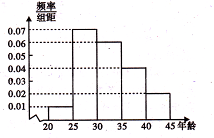 (2013•内江一模)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
(2013•内江一模)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示: