题目内容
若存在x∈[-| π |
| 3 |
| π |
| 4 |
| a |
| 2 |
分析:根据正弦函数的单调性,分别求出当0≤x≤
和-
≤x≤0时|sinx|的范围,进而推知x∈[-
,
]时,|sinx|的最大值.进而可知要使|sinx|>
成立,只需
小于其最大值即可.
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| a |
| 2 |
| a |
| 2 |
解答:解:当0≤x≤
时,0≤|sinx|=sinx≤
当-
≤x≤0时,0≤sinx|=-sinx≤
即当x∈[-
,
],0≤|sinx|≤
∴要使|sinx|>
成立,则需
<
即a<
故答案为:a<
| π |
| 4 |
| ||
| 2 |
当-
| π |
| 3 |
| ||
| 2 |
即当x∈[-
| π |
| 3 |
| π |
| 4 |
| ||
| 2 |
∴要使|sinx|>
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
即a<
| 3 |
故答案为:a<
| 3 |
点评:本题主要考查了正弦函数的单调性.属基础题.

练习册系列答案
相关题目
 时,若存在x∈[-3,-1]使得f′(x)>0成立,求b的取值范围;
时,若存在x∈[-3,-1]使得f′(x)>0成立,求b的取值范围;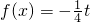 在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.
在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.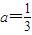 时,若存在x∈[-3,-1]使得f′(x)>0成立,求b的取值范围;
时,若存在x∈[-3,-1]使得f′(x)>0成立,求b的取值范围;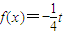 在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.
在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.