题目内容
【题目】在矩形ABCD中,对角线AC分别与AB,AD所成的角为α,β,则sin2α+sin2β=1,在长方体ABCD﹣A1B1C1D1中,对角线AC1与棱AB,AD,AA1所成的角分别为α1,α2,α3,与平面AC,平面AB1,平面AD1所成的角分别为β1,β2,β3,则下列说法正确的是( )
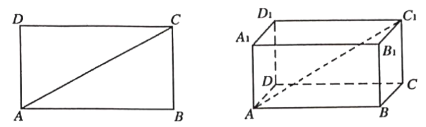
①sin2α1+sin2α2+sin2α3=1 ②sin2α1+sin2α2+sin2α3=2
③cos2α1+cos2α2+cos2α3=1 ④sin2β1+sin2β2+sin2β3=1
A. ①③B. ②③C. ①③④D. ②③④
【答案】D
【解析】
由已知条件,分别确定各个角的三角函数值,进而判断各个命题的真假,可得答案
(1)![]()
![]()
![]()
![]()
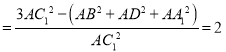 ,
,
所以,①错,②对;
(2)![]()
![]()
![]()
![]() ,
,
所以,③对
(3)![]()
![]() ,所以,④对
,所以,④对
答案选D

练习册系列答案
相关题目

