题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1\\;|x|≤2}\\{-2\\;|x|>2}\end{array}\right.$,求函数f(x)的定义域和值域.分析 |x|≤2,从而可得到x2+1≤5,即此时1≤f(x)≤5,而根据f(x)解析式,|x|>2时,f(x)=-2,从而把这两种情况下的f(x)的范围求并集即可得出原函数的值域.
解答 解:|x|≤2时,f(x)=x2+1≤5,且f(x)≥1;
|x|>2时,f(x)=-2;
∴原函数的值域为{f(x)|1≤f(x)≤5,或f(x)=-2}.
点评 考查函数值域的概念,分段函数值域的求法,以及不等式的性质:同向正的不等式两边平方后,不等号方向不变.

练习册系列答案
相关题目
8.把一个底面周长为4π,高为10的圆柱形铁块熔铸成底面积为20的圆锥,则这个圆锥的高为( )
| A. | 6 | B. | 6π | C. | 12 | D. | 12π |
9.已知有穷数列5,7,9,…,2n+7(n为偶数),则9+n是该数列的( )
| A. | 第n+1项 | B. | 第n+2项 | C. | 第$\frac{n}{2}$+2项 | D. | 第$\frac{n}{2}$+3项 |
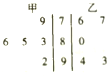 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论: