题目内容
15.已知数列{an}的前n项和为Sn,且点(n,Sn)在函数f(x)=1-($\frac{1}{2}$)x的图象上.(1)求数列{an}的通项公式;
(2)设bn=|log2an|,记Tn=$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$,若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,求实数m取值范围.
分析 (1)由点(n,Sn)在函数f(x)=1-($\frac{1}{2}$)x的图象上.可得Sn=1-$(\frac{1}{2})^{n}$,利用递推式 即可得出.
(2)bn=n,可得$\frac{{b}_{n}}{{a}_{n}}$=n•2n.利用“错位相减法”与等比数列的前n项和公式可得Tn,代入(n-1)2≤m(Tn-n-1)化简整理,再利用数列的单调性即可得出.
解答 解:(1)∵点(n,Sn)在函数f(x)=1-($\frac{1}{2}$)x的图象上.
∴Sn=1-$(\frac{1}{2})^{n}$,
当n=1时,a1=S1=1-$\frac{1}{2}$=$\frac{1}{2}$;
当n≥2时,an=Sn-Sn-1=$1-(\frac{1}{2})^{n}$-$[1-(\frac{1}{2})^{n-1}]$=$(\frac{1}{2})^{n}$.
当n=1时,上式也成立.
∴an=$(\frac{1}{2})^{n}$.
(2)bn=|log2an|=n,
∴$\frac{{b}_{n}}{{a}_{n}}$=n•2n.
∴Tn=$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$=2+2•22+3×23+…+(n-1)•2n-1+n×2n,
2Tn=22+2×23+3×24+…+(n-1)×2n+n×2n+1,
∴-Tn=2+22+23+…+2n-n×2n+1=$\frac{2({2}^{n}-1)}{2-1}$-n×2n+1=(1-n)×2n+1-2,
∴Tn=(n-1)×2n+1+2.
∴Tn-n-1=(n-1)×2n+1+2-n-1=(n-1)×(2n+1-1)>0(n≥2).
由(n-1)2≤m(Tn-n-1)即(n-1)2≤m(n-1)(2n+1-1).
由于上式对于n≥2恒成立,
∴m≥$\frac{n-1}{{2}^{n+1}-1}$≥$\frac{2-1}{{2}^{2+1}-1}$=$\frac{1}{7}$.
∴实数m取值范围是$[\frac{1}{7},+∞)$.
点评 本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、数列的单调性、不等式的性质、对数的运算性质,考查了推理能力与计算能力,属于中档题.

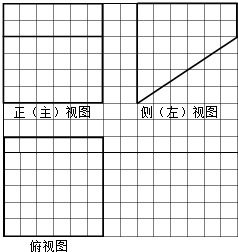 如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积是( )| A. | 128+12$\sqrt{13}$ | B. | 132+12$\sqrt{13}$ | C. | 144+12$\sqrt{13}$ | D. | 168 |
| A. | a≥0 | B. | a>0 | C. | a≤0 | D. | a<0 |