题目内容
(本小题12分)如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.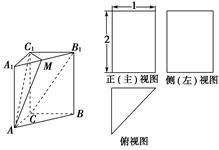
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
(1) 由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形,从而可知MO∥B1C,利用线面的平行的判定定理,得到结论。
(2)根据题意,由于MO∥B1C,同时能结合性质可知平面A1B1C1⊥平面AA1B1B,从而利用面面垂直的性质定理得到。
解析试题分析:(1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形,且∠ACB=90°.
连结A1C,设A1C∩AC1=O,连结MO,
由题意可知,A1O=CO,A1M=B1M,
∴MO∥B1C,
又MO?平面AC1M,
B1C?平面AC1M,∴B1C∥平面AC1M.
(2)∵A1C1=B1C1,M为A1B1的中点,
∴C1M⊥A1B1,
又平面A1B1C1⊥平面AA1B1B,
平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B,
考点:空间中线面和面面的位置关系
点评:解决的关键是是熟练的运用性质定理和判定定理,来证明,属于基础题。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
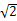 ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3
 到平面EA1C1的距离.
到平面EA1C1的距离. 分别是
分别是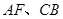 中点
中点
 .
.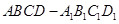 的底面边长为2,
的底面边长为2, .
.
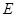 为线段
为线段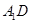 的中点,求
的中点,求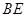 与平面
与平面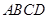 所成角的大小.
所成角的大小.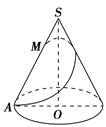
 中,
中, 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且 ,
, ,
, 为
为 的中点.
的中点.
 平面
平面 ;
; 与
与 所成角的正切值 .
所成角的正切值 . ,且
,且 ,
, 分别为
分别为 、
、 、
、 的中点
的中点
 的大小为
的大小为 ?若存在,求出CQ的长;若不存在,请说明理由。
?若存在,求出CQ的长;若不存在,请说明理由。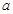 ,BC=CD=BD,设
,BC=CD=BD,设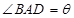 .
.
 的函数;
的函数; 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求  的值;
的值;