题目内容
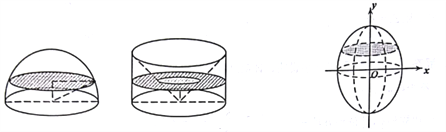
【题目】我国南北朝时间著名数学家祖暅提出了祖暅原理：“幂势既同，则积不容异”.意思是：夹在两平行平面间的两个几何体，被平行于这两个平行平面的任何平面所载，若截得的两个截面面积总相等，则这两个几何体的体积相等.为计算球的体积，构造一个底面半径和高都与球半径相等的圆柱，然后再圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥，运用祖暅原理可证明此几何体与半球体积相等（任何一个平面所载的两个截面面积都相等）.将椭圆
绕
轴旋转一周后得一橄榄状的几何体，类比上述方法，运用祖暅原理可求得其体积等于（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】分析：首先类比球的体积的求解方法构造出几何体，然后利用祖暅原理求解该几何体的体积即可.
详解：如图所示，椭圆的长半轴为4，短半轴为3.
现构造一个底面半径为3，高为4的圆柱，
然后在圆柱内挖去一个以圆柱下底面圆心为顶点，
圆柱上底面为底面的圆锥，当截面距离下底面的高度为h时，
设橄榄状的几何体对应的截面平径为R，圆柱对应截面的小圆半径为r，
则由
可得
，
则橄榄状的几何体对应的截面面积
.
由相似可得：
，即
，
圆柱对应的截面的面积
，
则
，由祖暅原理可得几何体的体积为：
.
本题选择C选项.
练习册系列答案
相关题目
