题目内容
【题目】选修4-4：坐标系与参数方程
已知曲线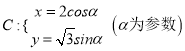
和定点
， 
是此曲线的左、右焦点，以原点
为极点，以
轴正半轴为极轴，建立极坐标系.
(1)求直线
的极坐标方程；
(2)经过点
且与直线
垂直的直线交此圆锥曲线于
两点，求
的值.
【答案】（1）
（2）
【解析】试题分析：（1）由圆锥曲线
化为
，可得
，利用截距式即可得出直线
的直角坐标方程，再化为极坐标方程即可；（2）直线
的斜率为
，可得直线
的斜率为直线
的方程为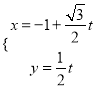
，代入椭圆的方程为
， 
，利用直线参数方程的几何意义及韦达定理可得结果.
试题解析：（1）曲线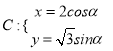
可化为
其轨迹为椭圆，焦点为
和
，经过
和
的直线方程为
所以极坐标方程为
（2）由（1）知直线
的斜率为
，因为
，所以
的斜率为
，倾斜角为
，所以
的参数方程为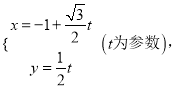
代入椭圆
的方程中，得
因为点
在
两侧，所以
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某学生对一些对数进行运算，如图表格所示：
x | 0.21 | 0.27 | 1.5 | 2.8 |
lgx | 2a+b+c﹣3（1） | 6a﹣3b﹣2（2） | 3a﹣b+c（3） | 1﹣2a+2b﹣c（4） |
x | 3 | 5 | 6 | 7 |
lgx | 2a﹣b（5） | a+c（6） | 1+a﹣b﹣c（7） | 2（a+c）（8） |
x | 8 | 9 | 14 | |
lgx | 3﹣3a﹣3c（9） | 4a﹣2b（10） | 1﹣a+2b（11） |
现在发觉学生计算中恰好有两次地方出错，那么出错的数据是（ ）
A.（3），（8）
B.（4），（11）
C.（1），（3）
D.（1），（4）
