题目内容
17.对于实数a,b,定义运算“*”:a*b=$\left\{\begin{array}{l}{-{a}^{2}+2ab-1.a<b}\\{{b}^{2}-ab,a>b}\end{array}\right.$,若f(x)=(2x-1)*(x-1),且函数y=f(x)-m有三个零点x1,x2,x3,则x1•x2•x3的取值范围是( )| A. | (-$\frac{1}{4}$,0) | B. | (-$\frac{1}{8}$,0) | C. | (-$\frac{1}{16}$,0) | D. | (-$\frac{1}{32}$,0) |
分析 由新定义求出函数的解析式,得到关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,实数m的取值范围及三个实根之间的关系,进而求出x1•x2•x3的取值范围.
解答 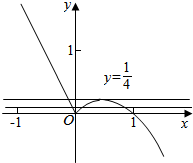 解:由2x-1<x-1,得x<0,此时f(x)=(2x-1)*(x-1)=-(2x-1)2+2(2x-1)(x-1)-1=-2x,
解:由2x-1<x-1,得x<0,此时f(x)=(2x-1)*(x-1)=-(2x-1)2+2(2x-1)(x-1)-1=-2x,
由2x-1>x-1,得x>0,此时f(x)=(2x-1)*(x-1)=(x-1)2-(2x-1)(x-1)=-x2+x,
∴f(x)=(2x-1)*(x-1)=$\left\{\begin{array}{l}{-2x,x<0}\\{-{x}^{2}+x,x>0}\end{array}\right.$,
作出函数的图象可得,
要使方程f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,不妨设x1<x2<x3,
则0<x2<$\frac{1}{2}$<x3<1,且x2和x3关于x=$\frac{1}{2}$对称,
∴x2+x3=2×$\frac{1}{2}$=1.则x2+x3≥2$\sqrt{{x}_{2}{x}_{3}}$,0<x2x3<$\frac{1}{4}$,等号取不到.
当-2x=$\frac{1}{4}$时,解得x=-$\frac{1}{8}$,
∴-$\frac{1}{8}$<x1<0,
∵0<x2x3≤$\frac{1}{4}$,
∴-$\frac{1}{32}$<x1•x2•x3<0,
即x1•x2•x3的取值范围是(-$\frac{1}{32}$,0).
故选:D.
点评 本题考查根的存在性及根的个数判断,根据已知新定义,求出函数的解析式并作出函数图象是解答的关键,是中档题.

练习册系列答案
相关题目