题目内容
15.函数f(x)=x2-4x-4在区间[t,t+1](t∈R)上的最小值记为g(t).(1)试写出g(x)的函数表达式;
(2)求g(t)的最小值.
分析 (1)配方法化简f(x)=x2-4x-4=(x-2)2-8,从而分类讨论以确定函数的解析式;
(2)分类讨论各段上的取值范围,从而求最小值的值.
解答 解:(1)f(x)=x2-4x-4=(x-2)2-8,
当t>2时,f(x)在[t,t+1]上是增函数,
∴g(t)=f(t)=t2-4t-4;
当t≤2≤t+1,即1≤t≤2时,
g(t)=f(2)=-8;
当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数,
∴g(t)=f(t+1)=t2-2t-7;
从而g(t)=$\left\{\begin{array}{l}{{t}^{2}-2t-7(t<1)}\\{-8(1≤t≤2)}\\{{t}^{2}-4t-4(t>2)}\end{array}\right.$;
(2)当t<1时,t2-2t-7>-8,
当t>2时,t2-4t-4>-8;
故g(t)的最小值为-8.
点评 本题考查了配方法的应用及分段函数的应用,同时考查了分类讨论的思想应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列命题中的说法正确的是( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ使得$\overrightarrow a=λ\overrightarrow b$ | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 命题“?x0∈R,使得${x_0}^2+{x_0}+1<0$”的否定是:“?x∈R,均有x2+x+1≥0” | |
| D. | “a≠5且b≠-5”是“a+b≠0”的充分不必要条件 |
10.已知α,β为不重合的两个平面,直线m?α,那么“m⊥β”是“α⊥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.在数列{an}中,a1=1,an+2+ancosnπ=1,记Sn是数列{an}的前n项和,则$\frac{{S}_{120}}{{a}_{61}}$等于( )
| A. | 930 | B. | 1520 | C. | 60 | D. | 61 |
4.设偶函数f(x)满足f(x)=2x-4(x≥0),若f(x-2)>0,则x的取值范围是( )
| A. | (-∞,0) | B. | (0,4) | C. | (4,+∞) | D. | (-∞,0)∪(4,+∞) |
5.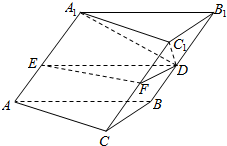 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )| A. | $\frac{{20\sqrt{2}}}{3}$ | B. | $\frac{{20\sqrt{3}}}{3}$ | C. | $\frac{{50\sqrt{2}}}{9}$ | D. | $\frac{{50\sqrt{3}}}{9}$ |