题目内容
5. 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )| A. | $\frac{{20\sqrt{2}}}{3}$ | B. | $\frac{{20\sqrt{3}}}{3}$ | C. | $\frac{{50\sqrt{2}}}{9}$ | D. | $\frac{{50\sqrt{3}}}{9}$ |
分析 作A1O⊥面ABC,垂足为O,连接AO,过O作OG⊥AC,垂足为G,连接A1G,由题意可知AO平分∠BAC,然后通过解直角三角形求得A1O,即三棱柱的高,再求出底面三角形的面积,由四棱锥D-A1C1EF的体积是原三棱柱体积的三分之一求得答案.
解答 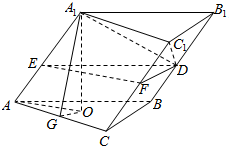 解:斜三棱柱ABC-A1B1C1,底面是边长为4的正三角形,侧棱长为5,
解:斜三棱柱ABC-A1B1C1,底面是边长为4的正三角形,侧棱长为5,
如图所示:
作A1O⊥面ABC,垂足为O,连接AO,
过O作OG⊥AC,垂足为G,连接A1G,
∵底面是边长为4的正三角形,侧棱AA1与底面相邻两边都成60°,
∴AO平分∠BAC,则∠OAG=30°,
∵A1O⊥面ABC,∴A1O⊥AG,
又OG⊥AG,且A1O∩OG=O,∴AG⊥平面A1OG,则AG⊥A1G.
设A1O=x,又AA1=5,得$AO=\sqrt{25-{x}^{2}}$,
∴$OG=\frac{1}{2}\sqrt{25-{x}^{2}}$,
在Rt△A1GA中,由AA1=5,∠A1AG=60°,得${A}_{1}G=\frac{5\sqrt{3}}{2}$.
在Rt△A1OG中,则${A}_{1}{O}^{2}+O{G}^{2}={A}_{1}{G}^{2}$,
∴${x}^{2}+(\frac{1}{2}\sqrt{25-{x}^{2}})^{2}=(\frac{5\sqrt{3}}{2})^{2}$,解得:$x=\frac{5\sqrt{6}}{3}$.
又${S}_{△ABC}=\frac{1}{2}×4×2\sqrt{3}=4\sqrt{3}$,
∴${V}_{D-{A}_{1}{C}_{1}FE}=\frac{1}{3}{S}_{△ABC}•{A}_{1}O$=$\frac{1}{3}×4\sqrt{3}×\frac{5\sqrt{6}}{3}=\frac{20\sqrt{2}}{3}$.
故选:A.
点评 本题考查了空间几何体的体积,考查数学转化思想方法,明确四棱锥D-A1C1EF的体积是原三棱柱体积的三分之一是关键,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | b<a<c | B. | a<b<c | C. | a<c<b | D. | c<a<b |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
| A. | S△AOC的最小值为$\frac{1}{2}$S | B. | SAOB的最小值为($\sqrt{2}$-1)S | ||
| C. | S△AOC+S△AOB的最大值为$\frac{1}{2}$S | D. | S△BOC的最大值为($\sqrt{2}$-1)S |
 已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.
已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l. 如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,
如图,长方体ABCD-A1B1C1D1的底面边长均为1,侧棱AA1=2,M,N分别是A1C1,A1A的中点,