题目内容
10.已知α,β为不重合的两个平面,直线m?α,那么“m⊥β”是“α⊥β”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 利用平面垂直的判定定理得到前者能推出后者;容易判断出后者推不出前者;利用各种条件的定义得到选项.
解答 解:∵平面垂直的判定定理:如果一个平面经过另一个平面的垂线,则两平面垂直
∴直线m?α,那么“m⊥β”成立时,一定有“α⊥β”成立
反之,直线m?α,若“α⊥β”不一定有“m⊥β”成立
所以直线m?α,那么“m⊥β”是“α⊥β”的充分不必要条件
故选:A
点评 本题考查平面垂直的判定定理、考查各种条件的定义并利用定义如何判定一个命题是另一个命题的什么条件.

练习册系列答案
相关题目
1.已知定义在R上的函数f(x)的图象是连续不断的,且有如下对应值表:
则函数f(x)一定存在零点的区间是( )
| x | 1 | 2 | 3 |
| f(x) | 3.4 | 2.6 | -3.7 |
| A. | (-∞,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
2.已知向量|$\overrightarrow{a}$|=2,(2$\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+2$\overrightarrow{b}$)=-1,向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,则|$\overrightarrow{b}$|等于( )
| A. | 1 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
20.两圆x2+y2=9和x2+y2-8x+6y+9=0的公切线条数是( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
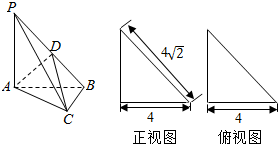 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为侧棱PB的中点,它的正视图和侧视图如图所示,给出下列结论
在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为侧棱PB的中点,它的正视图和侧视图如图所示,给出下列结论