Question

【题目】开发商现有四栋楼A，B，C，D．楼D位于BC间，到楼A，B，C的距离分别为，，，且从楼D看楼A，B的视角为．如图所示，不计楼大小和高度．

（1）试求从楼A看楼B，C视角大小；

（2）开发商为谋求更大开发区域，拟再建三栋楼M，P，N，形成以楼AMPN为顶点的矩形开发区域，规划要求楼B，C分别位于楼MP和楼PN间，如图所示，记，当等于多少时，矩形开发区域面积最大？

Answer 1

【答案】（1）从楼A看楼B，C视角的大小为； （2）

【解析】

（1）利用三角函数定义及边角关系，结合正切函数和角公式，即可求得楼A看楼B，C视角大小；

（2）由，利用直角三角形的边角关系，表示出矩形的面积，结合余弦差角公式及辅助角公式化简三角函数式，即可由正弦函数性质求得最大值.

（1）因为楼D到楼B、C的距离分别为和，到楼A的距离为，

所以百米，百米，百米，

因为从楼D看楼A、B的视角为，则，

则，,

所以

，

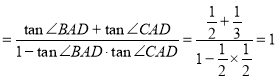又，

即，所以，

则从楼A看楼B，C视角的大小为；

（2）在和中，

，，

则在中，，

在中，，

记矩形开发区的面积为，

则

；

又

；

当时，即时，矩形开发区域AMPN的面积最大．