题目内容
设函数f(x)=sinxcosx﹣ cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按 =(
=(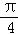 ,
,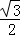 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,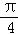 ]上的最大值.
]上的最大值.
 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按
 =(
=(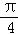 ,
,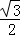 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,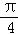 ]上的最大值.
]上的最大值.(1)π(2)

试题分析:(1)先利用诱导公式,二倍角公式与和角公式将函数解析式化简整理,然后利用周期公式可求得函数的最小正周期.
(2)由(1)得函数y=f(x),利用函数图象的变换可得函数y=g(x)的解析式,通过探讨角的范围,即可的函数g(x)的最大值.
解:(1)∵f(x)=sinxcosx﹣
 cos(x+π)cosx
cos(x+π)cosx=sinxcosx+
 cosxcosx
cosxcosx=
 sin2x+
sin2x+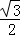 cos2x+
cos2x+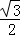
=sin(2x+
 )+
)+
∴f(x)的最小正周期T=
 =π
=π(2)∵函数y=f(x)的图象按
 =(
=(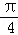 ,
, )平移后得到的函数y=g(x)的图象,
)平移后得到的函数y=g(x)的图象,∴g(x)=sin(2x+
 ﹣
﹣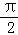 )+
)+ +
+ =sin(2x﹣
=sin(2x﹣ )+
)+
∵0<x≤
 ∴
∴ <2x﹣
<2x﹣ ≤
≤ ,
,∴y=g(x)在(0,
 ]上的最大值为:
]上的最大值为: .
.点评:本题考查了三角函数的周期及其求法,函数图象的变换及三角函数的最值,各公式的熟练应用是解决问题的根本,体现了整体意识,是个中档题.

练习册系列答案
相关题目

 的值;
的值; 时,求函数
时,求函数 的值域.
的值域. 的方程
的方程 在区间
在区间 上有两个不同的实数解,则实数
上有两个不同的实数解,则实数 的取值范围为 .
的取值范围为 . 的图像,
的图像, 是图像上任意一点,过点A作
是图像上任意一点,过点A作 轴的平行线,交其图像于另一点B(A,B可重合),设线段AB的长为
轴的平行线,交其图像于另一点B(A,B可重合),设线段AB的长为 ,则函数
,则函数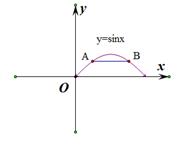




 ]上递减,且有最小值1,则ω的值可以是( )
]上递减,且有最小值1,则ω的值可以是( )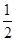

 的最大值与最小值之和为( )。
的最大值与最小值之和为( )。


 (
( )的大致图象是( )
)的大致图象是( )
 sinωx-sin2
sinωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.  ,
, R,则f(x)是( )
R,则f(x)是( ) 的奇函数
的奇函数 的奇函数
的奇函数