题目内容
(本小题满分13分) 已知抛物线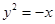 与直线
与直线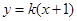 相交于
相交于 两点.
两点.
(1)求证:以 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点 ;(2)当
;(2)当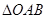 的面积等于
的面积等于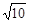 时,求
时,求 的值.
的值.
(1)见解析(2)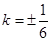
解析试题分析:(1)证明:由方程组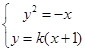 ,消去
,消去 整理得:
整理得: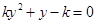 ,
,
设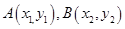 ,由韦达定理得:
,由韦达定理得: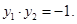
∵ 在抛物线
在抛物线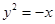 上,∴
上,∴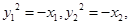
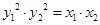 .
.
∵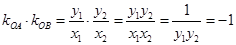 ,∴OA⊥OB.
,∴OA⊥OB.
故以 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点 . ……6分
. ……6分
(2)解:设直线与 轴交于
轴交于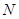 ,又显然
,又显然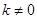 ,∴令
,∴令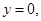 则
则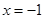 ,即
,即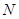 (-1,0).
(-1,0).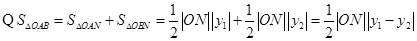 ,
,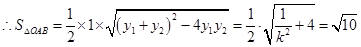 ,解得
,解得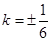 . ……13分
. ……13分
考点:本小题综合考查了直线与抛物线的位置关系、弦长公式及圆、三角形面积公式,考查了学生数形结合思想和划归思想及运算求解能力.
点评:直线与圆锥曲线的相交问题一般是联立方程组,设而不求,借助根的判别式及根与系数的关系进行转化.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
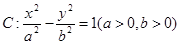 的离心率为
的离心率为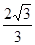 ,且过点P(
,且过点P(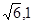 ).
).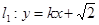 与双曲线C恒有两个不同的交点A,B,且
与双曲线C恒有两个不同的交点A,B,且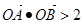
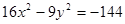 的焦点坐标,离心率和渐近线方程.
的焦点坐标,离心率和渐近线方程.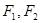 是双曲线
是双曲线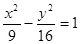 的两个焦点,点
的两个焦点,点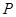 在双曲线上,且
在双曲线上,且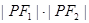
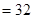 ,求证:
,求证: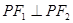
 的两个焦点分别为
的两个焦点分别为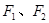 ,离心率为2.
,离心率为2. 的方程;
的方程; 、
、 分别为
分别为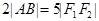 ,求线段
,求线段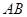 的中点
的中点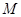 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线;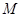 与直线
与直线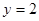 相切,且与定圆
相切,且与定圆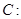
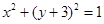 外切,求动圆圆心
外切,求动圆圆心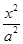 +
+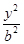 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,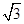 ,
,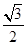 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.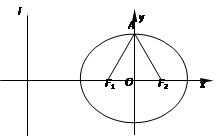
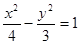 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于 轴的弦,
轴的弦,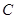 的方程;
的方程;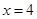 与
与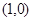 ,求证:
,求证: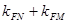 为定值;
为定值;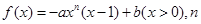 为正整数,
为正整数,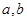 为常数.曲线
为常数.曲线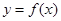 在点
在点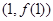 处的切线方程为
处的切线方程为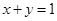 .
.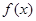 的最大值;
的最大值;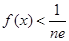 .
.