题目内容
如图,在直三棱柱ABC —A1B1C1 中,AB = AC = 1,AA1 = 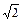 ,AB⊥AC
,AB⊥AC 求异面直线BC1与AC所成角的度数
求异面直线BC1与AC所成角的度数
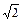 ,AB⊥AC
,AB⊥AC 求异面直线BC1与AC所成角的度数
求异面直线BC1与AC所成角的度数
解:在直三棱柱ABC—A1B1C1中,AC // A1C1 ,∴∠B C1A1就是BC1
 与AC所成的角
与AC所成的角 …2分连结A1B,在△A1B C1中,由已知得BA1=
…2分连结A1B,在△A1B C1中,由已知得BA1=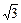 ,
,
A1C1=1,BC1="2" ,…2分由余弦定理得cos∠BC1A1=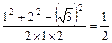 ,
,
∴∠B C1A1=60°,…3分因此直线BC1与AC所成的角为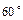
 与AC所成的角
与AC所成的角 …2分连结A1B,在△A1B C1中,由已知得BA1=
…2分连结A1B,在△A1B C1中,由已知得BA1=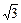 ,
,A1C1=1,BC1="2" ,…2分由余弦定理得cos∠BC1A1=
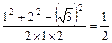 ,
,∴∠B C1A1=60°,…3分因此直线BC1与AC所成的角为
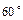
略

练习册系列答案
相关题目
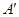 的位置,且
的位置,且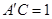 ,则折起后二面角
,则折起后二面角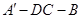 的大小 ( )
的大小 ( )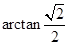
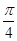
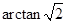
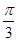

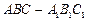 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是 的中点,直线
的中点,直线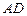 与侧面
与侧面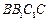 所成的角是
所成的角是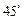 .
.
 的大小;
的大小;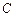 到平面
到平面 的距离.
的距离.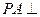 平面ABC,
平面ABC, 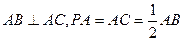 ,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。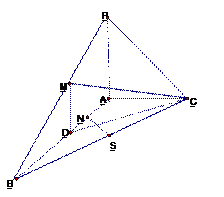
 平面CDM.
平面CDM. 分10分)
分10分) B1C1D1中,AA1 =
B1C1D1中,AA1 =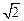 ,AB = 1,E是DD1的中点.
,AB = 1,E是DD1的中点.
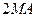 =
=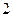

 ,则在
,则在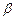 内过点B的所有直线中( )
内过点B的所有直线中( )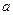 平行的直线
平行的直线 ,若侧棱
,若侧棱 ,则正三棱锥S—ABC外接球的表面积是()
,则正三棱锥S—ABC外接球的表面积是()

 .36
.36