题目内容
(本小题满分12分)
如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。

(1)求证:MN是AB和PC的公垂线
(2)求异面直线AB和PC之间的距离
如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。

(1)求证:MN是AB和PC的公垂线
(2)求异面直线AB和PC之间的距离
解:(1)连结AN,B N,∵△APC
N,∵△APC 与△BPC是全等的正三角形,又N
与△BPC是全等的正三角形,又N 是PC的中点
是PC的中点
∴AN=BN
又∵M是AB的中点,∴MN⊥AB ……… 3分
同理可证MN⊥PC, 又∵MN∩AB=M,MN∩PC="N "
∴MN是AB和PC的公垂线。 ……… 6分
(2)在等腰三角形ANB中,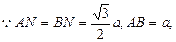 ……… 8分
……… 8分

即异面直线AB和PC之间的距离为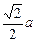 .……… 12分
.……… 12分
 N,∵△APC
N,∵△APC 与△BPC是全等的正三角形,又N
与△BPC是全等的正三角形,又N 是PC的中点
是PC的中点∴AN=BN
又∵M是AB的中点,∴MN⊥AB ……… 3分
同理可证MN⊥PC, 又∵MN∩AB=M,MN∩PC="N "
∴MN是AB和PC的公垂线。 ……… 6分
(2)在等腰三角形ANB中,
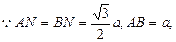 ……… 8分
……… 8分
即异面直线AB和PC之间的距离为
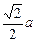 .……… 12分
.……… 12分略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 中,
中,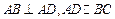 ,
,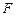 为
为 的中点,
的中点, 在
在 上,且
上,且 。已知
。已知 ,沿线段
,沿线段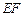 把四边形
把四边形 折起如图b,使平面
折起如图b,使平面 。
。
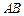 ⊥平面
⊥平面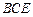 ;
; 体积.
体积.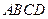 是
是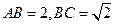 的矩形,
的矩形,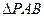 是正三角形,将
是正三角形,将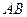 折起,使
折起,使 如图2,
如图2,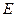 为
为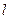 过点
过点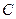 且垂直于矩形
且垂直于矩形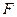 是直线
是直线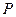 位于平面
位于平面
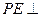 平面
平面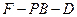 的平面角为
的平面角为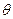 ,若
,若 ,求线段
,求线段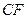 长的取值范围。
长的取值范围。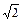 ,AB⊥AC
,AB⊥AC 求异面直线BC1与AC所成角的度数
求异面直线BC1与AC所成角的度数

 ,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.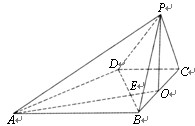
 大小;
大小;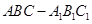 中,底面边长和侧棱都是2,D是侧棱
中,底面边长和侧棱都是2,D是侧棱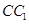 上任意一点.E是
上任意一点.E是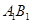 的中点.
的中点.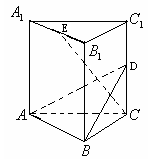
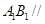 (1)求证: 平面ABD;
(1)求证: 平面ABD;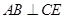 (2)求证: ;
(2)求证: ;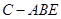 的体积。
的体积。