题目内容
.如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=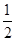 .
.
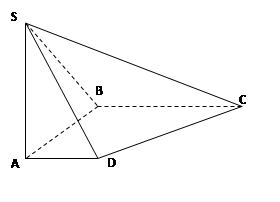
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC;
(3)求二面角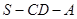 的正切值.
的正切值.
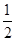 .
.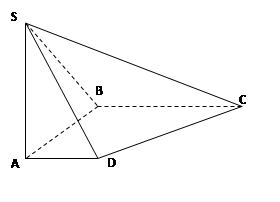
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC;
(3)求二面角
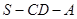 的正切值.
的正切值. (1)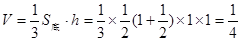 ;
;
(2)证明:见解析;(3)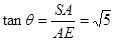 。
。
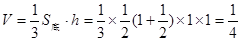 ;
;(2)证明:见解析;(3)
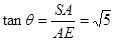 。
。(1)根据棱锥的体积公式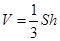 直接求解即可.
直接求解即可.
(2)根据面面垂直的判定定理,只需证明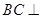 平面
平面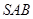 .
.
(3)解决本小题的关键是做(找)出二面角的平面角.过点 作
作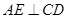 于
于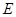 (
(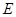 在
在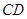 的延长线上,连接
的延长线上,连接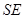 ,则
,则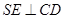 ,所以
,所以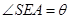 为二面角
为二面角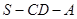 的平面角.
的平面角.
(1)由棱锥体积公式: ----------4分
----------4分
(2)证明: ,
,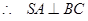 ,
,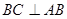 ,
,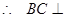 平面
平面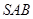
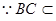 平面
平面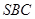 ,
,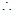 面SAB⊥面SBC -----------8分
面SAB⊥面SBC -----------8分
(3)过点 作
作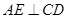 于
于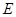 (
(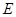 在
在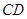 的延长线上,连接
的延长线上,连接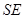 ,则
,则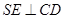 ,所以
,所以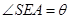 为二面角
为二面角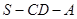 的平面角.-------------------10分
的平面角.-------------------10分
在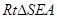 中,
中,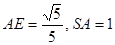 ,所以
,所以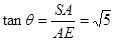 ------------12分
------------12分
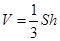 直接求解即可.
直接求解即可.(2)根据面面垂直的判定定理,只需证明
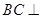 平面
平面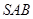 .
.(3)解决本小题的关键是做(找)出二面角的平面角.过点
 作
作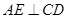 于
于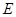 (
(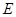 在
在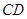 的延长线上,连接
的延长线上,连接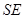 ,则
,则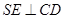 ,所以
,所以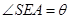 为二面角
为二面角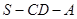 的平面角.
的平面角.(1)由棱锥体积公式:
 ----------4分
----------4分(2)证明:
 ,
,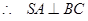 ,
,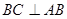 ,
,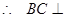 平面
平面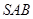
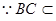 平面
平面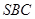 ,
, 面SAB⊥面SBC -----------8分
面SAB⊥面SBC -----------8分(3)过点
 作
作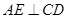 于
于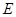 (
(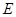 在
在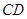 的延长线上,连接
的延长线上,连接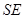 ,则
,则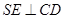 ,所以
,所以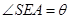 为二面角
为二面角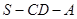 的平面角.-------------------10分
的平面角.-------------------10分在
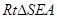 中,
中,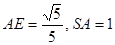 ,所以
,所以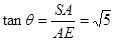 ------------12分
------------12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
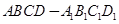 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,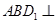 平面
平面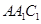
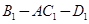 的平面角为120°时,求四棱锥
的平面角为120°时,求四棱锥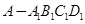 的体积。
的体积。

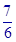
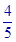
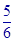
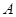 .
.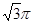
 .
.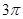
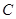 .
.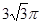
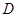 .
.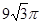
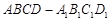 中,
中,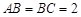 ,过
,过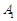 、
、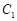 、
、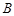 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体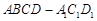 ,且这个几何体的体积为
,且这个几何体的体积为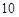 .
.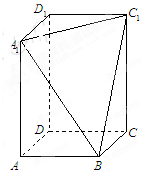
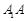 的长;
的长;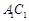 的中点为
的中点为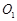 ,求异面直线
,求异面直线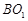 与
与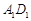 所成角的余弦值.
所成角的余弦值.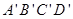 中,AB=1,
中,AB=1,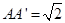 ,则A,C两点间的球面距离为( )
,则A,C两点间的球面距离为( ) 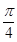
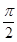
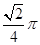
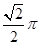
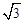 正方形。若PA=2
正方形。若PA=2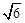 ,则△OAB的面积为______________.
,则△OAB的面积为______________.