题目内容
【题目】已知函数f(x)=|x﹣a|+2|x+b|(a>0,b>0)的最小值为1.
(1)求a+b的值;
(2)若 ![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
【答案】
(1)解: 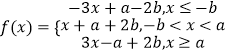
f(x)在区间(﹣∞,﹣b]上递减,在区间[﹣b,+∞)上递增,
所以f(x)min=a+b.
所以a+b=1.
(2)解:因为a>0,b>0,且a+b=1,
所以 ![]() ,
,
又因为 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,
时,等号成立,
所以 ![]() 时,
时, ![]() 有最小值
有最小值 ![]() .
.
所以 ![]() ,所以实数m的最大值为
,所以实数m的最大值为 ![]()
【解析】(1)写出分段函数,得出f(x)min=a+b,即可求a+b的值;(2)因为a>0,b>0,且a+b=1,利用“1”的代换,求最值,根据 ![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.

练习册系列答案
相关题目
【题目】“微信运动”已成为当下热门的健身方式,小明的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
| 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 |
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)若采用样本估计总体的方式,试估计小明的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步时被系统评定为“积极型”,否则为“懈怠型”.根据小明的统计完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |