题目内容
已知抛物线
与直线
相交于A、B两点，其中A点的坐标是(1，2)。如果抛物线的焦点为F，那么
等于（ ）
A． 5 B．6 C． 
D．7
D
解析试题分析：把点（1，2），代入抛物线和直线方程，分别求得p=2，a=2
∴抛物线方程为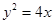
，直线方程为2x+y-4=0，联立消去y整理得
，解得x和1或4，
∵A的横坐标为1，∴B点横坐标为4，根据抛物线定义可知|FA|+|FB|=
+1+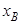
+1=7，故选D．.
考点：直线与圆锥曲线的关系；直线的一般式方程；抛物线的简单性质．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
轴上，且长轴长为12，离心率为
，则椭圆的方程是( )
与圆
，若在椭圆
上存在点P，使得由点P所作的圆
的两条切线互相垂直，则椭圆
已知双曲线
:
(
)的离心率为
,则的渐近线方程为( )
A． | B． | C． | D． |
设
、
分别是椭圆
的左、右焦点，点
在椭圆
上，线段
的中点在
轴上，若
，则椭圆的离心率为（ ）
A． | B． | C． | D． |
设
是双曲线
的两个焦点, 
是
上一点,若
且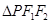
的最小内角为
,则的离心率为( )
A． | B． | C． | D． |
的左、右焦点．若点P在双曲线上，且
·
＝0，则|
抛物线
的准线为( )
| A．x= 8 | B．x=-8 |
| C．x=4 | D．x=-4 |
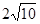
（a>0,b>0）的左右焦点分别为F1，F2，渐近线分别为l1，l2，点P在第一象限内且在l1上，若l2⊥PF1，l2∥PF2，则该双曲线的离心率为（ ）
