Question

【题目】已知椭圆，四点、、、中恰有三点在椭圆上。

（1）求的方程：

（2）椭圆上是否存在不同的两点、关于直线对称？若存在，请求出直线的方程，若不存在，请说明理由；

（3）设直线不经过点且与相交于、两点，若直线与直线的斜率的和为1，求证：过定点。

Answer 1

【答案】（1）（2）

【解析】

(1) 结合椭圆几何特征，可得、、在椭圆上，解方程即得椭圆的方程.(2) 设直线为，线段中点为，利用椭圆的中点弦性质求得中点，即得m=-.(3) 设，根据已知得到所以直线，即得直线经过的定点坐标.

（1）结合椭圆几何特征，可得、、在椭圆上，所以b=1,,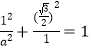

解得方程为.

（2）设直线为，线段中点为，根据椭圆中点弦性质，，联立解得中点，

（3）设，联立得，

直线，所以k(x+2)-1-y=0,所以x+2=0且-1-y=0,所以x=-2,y=-1,

所以直线经过定点.