题目内容
【题目】给出下列四个命题
①已知
为椭圆
上任意一点，
，
是椭圆的两个焦点，则
的周长是8；
②已知
是双曲线
上任意一点，
是双曲线的右焦点，则
；
③已知直线
过抛物线
的焦点，且与
交于
，
，
，
两点，则
；
④椭圆具有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点，是它的焦点，长轴长为
，焦距为
，若静放在点的小球（小球的半径忽略不计）从点沿直线出发则经椭圆壁反射后第一次回到点时，小球经过的路程恰好是
．
其中正确命题的序号为__（请将所有正确命题的序号都填上）
【答案】②③
【解析】
①求得椭圆中的
， 
，
的周长为：
，即可判断；
②求得双曲线中的，
，，讨论
在双曲线的左支或右支上，求得最小值，即可判断；
③设出直线
的方程，代入抛物线方程，运用韦达定理，即可判断；
④可假设长轴在
，短轴在
轴，对球的运动方向沿轴向左直线运动，沿轴向右直线运动，以及球不沿轴运动，讨论即可.
①由椭圆方程
，得
，
，因
为椭圆上任意一点，由椭圆定义知，的周长为
，故①错误；
②已知是双曲线
上任意一点，且，
，
是双曲线的右焦点，若在双曲线左支上，则
，若在双曲线右支上，则
，故②正确；
③直线过抛物线
的焦点，设其方程为
，
，
，将直线代入抛物线的方程可得
，由韦达定理可得
，又
，则
，故③正确；
④假设长轴在，短轴在轴，设
为左焦点，
为左焦点，以下分为三种情况：
i．球从 沿轴向左直线运动，碰到左顶点必然原路反弹，这时第一次回到路程
是
；
ii．球从沿轴向右直线运动，碰到右顶点必然原路反弹，这时第一次回到路程
是
；
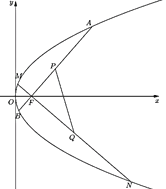
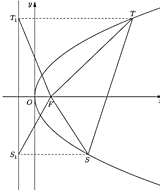
iii．球从不沿轴斜向上（或向下）运动，碰到椭圆上的点
，反弹后经过椭圆的另一个焦点，再弹到椭圆上一点
，经反弹后经过点，此时小球经过的路程是
；
综上所述：从点沿直线出发，经椭圆壁反弹后第一次回到时，小球经过的路程是或或.故④错误.
故答案为：②③.
