题目内容
已知函数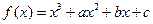 在
在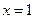 与
与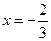 时,都取得极值。
时,都取得极值。
(1)求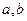 的值;
的值;
(2)若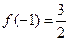 ,求
,求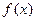 的单调区间和极值;
的单调区间和极值;
(3)若对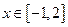 都有
都有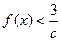 恒成立,求
恒成立,求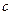 的取值范围。
的取值范围。
解:(1)f ′(x)=3x2+2a x+b=0.
由题设,x=1,x=-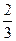 为f ′(x)=0的解.
为f ′(x)=0的解.
-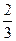 a=1-
a=1-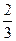 ,
,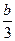 =1×(-
=1×(-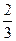 ).∴a=-
).∴a=-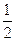 ,b=-2……………………………………4分
,b=-2……………………………………4分
经检验得:这时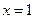 与
与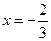 都是极值点.…………………………………5分
都是极值点.…………………………………5分
(2)f (x)=x3-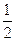 x2-2 x+c,由f (-1)=-1-
x2-2 x+c,由f (-1)=-1-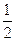 +2+c=
+2+c=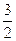 ,c=1.
,c=1.
∴f (x)=x3-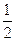 x2-2 x+1.
x2-2 x+1.
∴ f (x)的递增区间为(-∞,-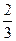 ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(-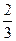 ,1).
,1).
当x=-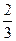 时,f (x)有极大值,f (-
时,f (x)有极大值,f (-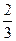 )=
)=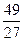 ;
;
当x=1时,f (x)有极小值,f (1)=-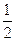 ……………………………………………10分
……………………………………………10分
(3)由(1)得,f ′(x)=(x-1)(3x+2),f (x)=x3-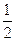 x2-2 x+c,
x2-2 x+c,
f (x)在[-1,-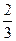
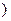 及(1,2]上递增,在(-
及(1,2]上递增,在(-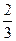 ,1)递减.
,1)递减.
而f (-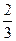 )=-
)=-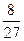 -
-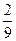 +
+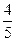 +c=c+
+c=c+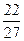 .f (2)=8-2-4+c=c+2.
.f (2)=8-2-4+c=c+2.
∴ f (x)在[-1,2]上的最大值为c+2.∴ 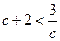 ,∴
,∴ 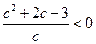
∴ 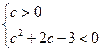 或
或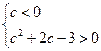 ∴
∴ 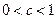 或
或 …………………16分
…………………16分
解析

练习册系列答案
相关题目
已知函数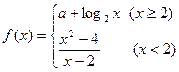 在点
在点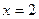 处连续,则常数
处连续,则常数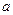 的值是
的值是
| A.2 | B.3 | C.4 | D.5 |
 ,
, .
. 的单调区间和最小值;
的单调区间和最小值; 的大小关系;
的大小关系;
 的取值范围,使得
的取值范围,使得 <
< 对任意
对任意 >0成立
>0成立 .
. ,
,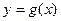 在
在 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程; 单调递增,求
单调递增,求 的取值范围.
的取值范围.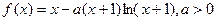 .
. 的单调区间;
的单调区间;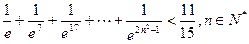 .
. .
.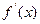 的解析式;
的解析式; ,讨论函数
,讨论函数 的单调性;
的单调性; ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 过点
过点 ,且与曲线
,且与曲线 和
和 都相切,
都相切, 的值。
的值。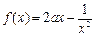 ,
, .
.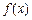 在
在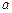 的取值范围;
的取值范围;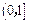 上的最大值.
上的最大值.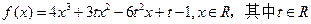 ,
,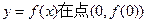 处的切线方程;
处的切线方程;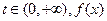 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。