题目内容
三棱锥P-ABC的高PO=8，AC=BC=3，∠ACB=30°，M、N分别在BC和PO上，且CM=x，PN=3CM，试问下面的四个图象中，那个图象大致描绘了三棱锥N-AMC的体积V与x的变化关系（x∈[0，3]）（ ）A．
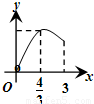
B．
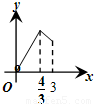
C．
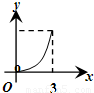
D．
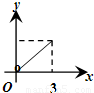
【答案】分析：由题意直接求出三棱锥N-AMC的体积V与x变化关系，通过函数表达式，确定函数的图象即可．
解答：解：底面三角形ABC的边AC=3，CM=x，∠ACB=30°，
∴△ACM的面积为：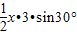
=
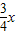
又∵三棱锥N-AMC的高NO=PO-PN=8-3x
所以三棱锥N-AMC的体积V=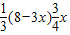
=
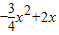
当x=
时取得最大值，开口向下的二次函数，
故选A．
点评：本题是基础题，考查几何体的体积与函数之间的关系，求出底面三角形的面积，是本题的一个关键步骤，通过二次函数研究几何体的体积的变化趋势是本题的特点，是好题，新颖题目．
解答：解：底面三角形ABC的边AC=3，CM=x，∠ACB=30°，
∴△ACM的面积为：
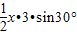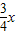
=又∵三棱锥N-AMC的高NO=PO-PN=8-3x
所以三棱锥N-AMC的体积V=
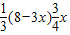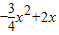
=当x=
时取得最大值，开口向下的二次函数，故选A．
点评：本题是基础题，考查几何体的体积与函数之间的关系，求出底面三角形的面积，是本题的一个关键步骤，通过二次函数研究几何体的体积的变化趋势是本题的特点，是好题，新颖题目．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目