题目内容
正三棱锥P-ABC的高PO=4，斜高为2| 5 |
分析：先求正三棱锥P-ABC的底面面积，再求经过PO的中点且平行于底面的截面的面积．
解答：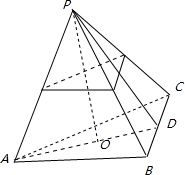
解：由题意正三棱锥P-ABC的高PO=4，斜高为2
，
可知OD=
=2AD=6
则AB=4
底面面积是12
中截面面积是
×12
=3
故答案为：3
解：由题意正三棱锥P-ABC的高PO=4，斜高为2| 5 |
可知OD=
(2
|
则AB=4
| 3 |
底面面积是12
| 3 |
中截面面积是
| 1 |
| 4 |
| 3 |
| 3 |
故答案为：3
| 3 |
点评：本题考查棱锥的结构特征，考查面积比是相似比的平方，是中档题．
练习册系列答案
相关题目