题目内容
三棱锥P-ABC的高为PH，若P到△ABC的三边的距离相等，若H在△ABC内，则H为△ABC的（ ）
分析：画出图形，利用三垂线逆定理证明三角形ABC中H为三角形的内心即可．
解答：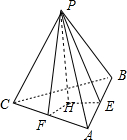
解：三棱锥P-ABC的高为PH，若P到△ABC的三边的距离相等，若H在△ABC内，
如图：做PE、PF、PG分别 垂直AB，AC，BC，则PE=PF=PG，连接HE，HF，HG，
由三垂线逆定理可知HE⊥AB，HF⊥AC，HG⊥BC，并且△PHE≌△PHF≌△PHG，
所以HG=HE=HF，所以H为三角形的内心．
故选A．
解：三棱锥P-ABC的高为PH，若P到△ABC的三边的距离相等，若H在△ABC内，如图：做PE、PF、PG分别 垂直AB，AC，BC，则PE=PF=PG，连接HE，HF，HG，
由三垂线逆定理可知HE⊥AB，HF⊥AC，HG⊥BC，并且△PHE≌△PHF≌△PHG，
所以HG=HE=HF，所以H为三角形的内心．
故选A．
点评：本题考查直线与平面垂直的判定定理的应用，三角形的全等，三角形的内心的判断方法，考查逻辑推理能力．
练习册系列答案
名校课堂系列答案
相关题目