题目内容
三棱锥P-ABC的高为PH，若三条侧棱相等，则H为△ABC的（ ）
分析：三棱锥P-ABC的高为PH，若PA=PB=PC，可证得△PHA≌△PHB≌△PHC，从而证得HA=HB=HC，符合这一性质的点H是△ABC外心．
解答：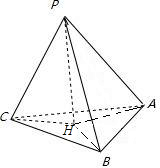
证明：三棱锥P-ABC的高为PH，若PA=PB=PC，
故△PHA，△PHB，△PHC都是直角三角形
∵PH是公共边，PA=PB=PC
∴△PHA≌△PHB≌△PHC
∴HA=HB=HC
故H是△ABC外心
故选B
证明：三棱锥P-ABC的高为PH，若PA=PB=PC，故△PHA，△PHB，△PHC都是直角三角形
∵PH是公共边，PA=PB=PC
∴△PHA≌△PHB≌△PHC
∴HA=HB=HC
故H是△ABC外心
故选B
点评：本题考查三角形五心，求解本题的关键是能够根据题设条件得出PA，PB，PC在底面上的射影相等，以及熟练掌握三角形个心的定义，本题是一个判断形题，是对基本概念的考查题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目