题目内容
17．如图，在⊙O中，AB=2CD．求证：$\widehat{AB}$＞2$\widehat{CD}$．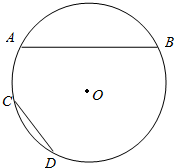
分析 过圆心O作OF垂直AB，交圆O于点E，则AF=BF=CD，证明$\widehat{AE}$＞$\widehat{CD}$，$\widehat{BE}$＞$\widehat{CD}$，即可证明结论．
解答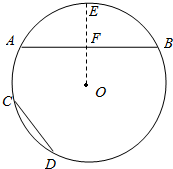 
证明：过圆心O作OF垂直AB，交圆O于点E，则AF=BF=CD，
而三角形AEF、三角形BEF都是直角三角形，那就有AE=BE＞AF=CD，即AE＞CD，BE＞CD，所以$\widehat{AE}$＞$\widehat{CD}$，$\widehat{BE}$＞$\widehat{CD}$，
从而就有$\widehat{AB}$=$\widehat{AE}$+$\widehat{BE}$＞$\widehat{CD}$+$\widehat{CD}$=2$\widehat{CD}$，即$\widehat{AB}$＞2$\widehat{CD}$．
点评 本题考查垂径定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目