题目内容
【题目】已知椭圆 
=1（a＞b＞0）的离心率为 
，坐标原点O到过点A（0，﹣b）和B（a，0）的直线的距离为 
．又直线y=kx+m（k≠0，m≠0）与该椭圆交于不同的两点C，D．且C，D两点都在以A为圆心的同一个圆上．
（1）求椭圆的方程；
（2）求△ABC面积的取值范围．
【答案】
（1）解：由椭圆 
=1（a＞b＞0）的焦点在x轴上，
离心率e= 
= 
，即2a2=3c2，
由题意可知：由△AOB的面积S= 
ab= 
，整理得：a2b2= 
（a2+b2），
a2=b2+c2，
解得：a2=3，b2=1，c2=1，
∴椭圆的方程 
（2）解：由（1）可知：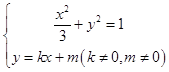 
，消去y整理得：（1+3k2）x2+6kmx+3m2﹣3=0，
△=36km﹣4（1+3k2）（3m2﹣3）＞0，解得：3k2＞m2﹣1，
设C（x1，y1），D（x2，y2）．CD的中点为P（x0，y0），
由韦达定理可知：x1+x2=﹣ 
，x1x2= 
，
则y1+y2=k（x1+x2）+2m= 
，
由中点坐标公式可知：x0=﹣ 
，y0= 
，
∴P（﹣ ， ）
依题意，可知AP⊥CD，
∴kAPkCD=﹣1，代入坐标，整理得：3k2=2m﹣1
由①③以及2m﹣1＞0，可解得： ＜m＜2，
由②③，根据弦长公式可知：丨CD丨= 
丨x1﹣x2丨= 
= 
点A到CD的距离d= 
，
∴S△ACD= d丨CD丨= 
，且 ＜m＜2，
令f（x）=x+ 
﹣x2（ ＜x＜2），
求导得′（x）=﹣ 
﹣2x＜0，
∴f（x）在（ ，2）上单调递减，
∴S△ACD∈（0， 
）．
△ABC面积的取值范围（0， ）．
【解析】（1）由椭圆 =1（a＞b＞0）的焦点在x轴上，则离心率e= = ，即2a2=3c2 ， 根据三角形面积相等，求得a2b2= （a2+b2），由a2=b2+c2 ， 即可求得a和b的值，求得椭圆的方程；（2）将直线方程代入椭圆方程，由△＞0，求得3k2＞m2﹣1，根据韦达定理可知：x1+x2=﹣ ，x1x2= ，利用中点坐标公式，求得P点坐标，由kAPkCD=﹣1，即可求得3k2=2m﹣1，代入，由弦长公式可知：丨CD丨= 丨x1﹣x2丨，点A到CD的距离d= ，则S△ACD= d丨CD丨= ＜m＜2，设f（x）=x+ ﹣x2（ ＜x＜2），求导，利用函数的单调性求得f（x）在（ ，2）上单调递减，即可求得△ABC面积的取值范围．
